Binary Example

What does Bayes Decision Rule have to do with Pattern Recognition?

Let’s consider a three dimensional binary feature vector X=(x₁,x₂,x₃) = (0,1,1) that we will attempt to classify with one of the following classes:

and lets say that the prior probability for class 1 is P(ω₁)= 0.6 while for class 2 is P(ω₂)= 0.4. Hence, it is already evident that there is a bias towards class 1.

Additionally, we know that likelihoods of each independent feature is given by p and q where:

p_i = P(x_i=1|ω₁) and q_i = P(x_i=1|ω₂)

meaning that we know the probability (or likelihood) of each independent feature given each class - these values are known and given:

p = {0.8, 0.2, 0.5} and q = {0.2, 0.5 , 0.9}

therefore, the discriminant function is g(x) = g₁(x) - g₂(x) or by taking the log of both sides:

however, since the problem definition assumes that X is independent, the discriminant function can be calculated by:

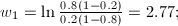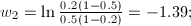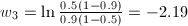
After inputting the x_i values into the discriminant function, the answer g(x) = -2.4849. Therefore this belongs to class 2. Below is a plot of the decision boundary surface.

 All points above the plane belong to class ω₂ since if X = (0,1,1), g(x) = -2.4849 < 0.

 Interested in plotting the above plane? Get the MatLab Mfile here: ThreeDBayesBoundary.m