About The Decision Rule
What, are you having trouble giving me an answer?
Then take a guess. Chances are, close to 50%
of you answered yes, and the other 50 answered no. Of course, given no
other information about
my state right now, it would be difficult for you to make a decision.
There is an equal probability
for me to have the flu or not. You might need to make an observation
first. For example, if I tell
you that my temperature is 42 degrees. I ask you again, Do I have the
flu?
Bayes decision making is about making a decision
about the state of nature based on how
probable that state is. In the above example, you want to decide
whether to diagnose me with the
flu based on how probable it is that I have it. Given that my
temperature is high, the odds of me
having the flu are now higher, but still not 100%, since it can be due
to other diseases for
example. Thus, the observation of my temperature gives you a better
idea about my state. Once
we have obtained an observation x, we can have a better idea about the
state of nature. Thus, the
probabilities of the current state of nature have changed due to our
observation.
In the above example, w1
is the state of having the flu and w2
is the state of not having the flu. As we saw, the probability of 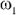 (p( (p(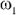 )) has
changed given the observations (i.e. p( )) has
changed given the observations (i.e. p(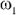 ) ) 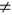 ( (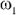 |x)
). If p( |x)
). If p(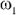 |x)
> p( |x)
> p(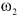 |x),
then the probability of the patient having the flu is higher than the
probability of the patient not having the flu, and you might be
inclined to decide that the patient has the flu. Of course, if you want
to be just a bit more careful you might want to run some medical exams
before making such a diagnosis, but let’s not complicate
things. If you decide on |x),
then the probability of the patient having the flu is higher than the
probability of the patient not having the flu, and you might be
inclined to decide that the patient has the flu. Of course, if you want
to be just a bit more careful you might want to run some medical exams
before making such a diagnosis, but let’s not complicate
things. If you decide on 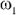 , there are chances that you make the wrong
decision. The probability of making the wrong decision is the same as
the probability that nature is at a different state that the one we
chose, that is the probability that the patient doesn’t have
the flu. In the case of deciding on , there are chances that you make the wrong
decision. The probability of making the wrong decision is the same as
the probability that nature is at a different state that the one we
chose, that is the probability that the patient doesn’t have
the flu. In the case of deciding on 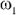 ,
the error is the probability of state ,
the error is the probability of state 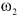 given the
observation x (p( given the
observation x (p(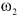 |x)). |x)).
Formally, the probability of error is:
So if we decide wi
and p(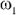 |
x) > p( |
x) > p(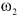 |
x), then we get a higher error than if we decide |
x), then we get a higher error than if we decide 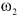 . Thus
deciding on the state that has the higher posterior probability
minimizes the probability of error. . Thus
deciding on the state that has the higher posterior probability
minimizes the probability of error.
If we generalize to more than 2 possible states,
and replace the observation x with a vector X,
minimizing the error rate corresponds to the following decision rule:
Discrete Case
The continuous case involved features vectors that
could be any point in Rd. For example, a feature can be the temperature
of a room and can have any value, including decimals. The discrete case
basically involves a limited or finite number of possible observations.
Thus, the feature vector x is no longer element of Rd. But can now have
m possible discrete values v1,…vm.
For example, a feature can be the state of a switch that can either be
on (1) or off (0). This leads to a few minor changes in the way the
decision rule is calculated, as we will see below.
- In the discrete case, the bayes decision rule
is unchanged. The probability density function p(x|
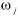 ) becomes
singular, and integrals are replaced by sums. For example, ) becomes
singular, and integrals are replaced by sums. For example,
|
|
is replaced by
|
|
|
where we sum the conditional probabilities for all possible values of x
in the discrete distribution. |
- Bayes formula involves probabilities instead of
probability densities.
|
|
|
|
|
|
| where |
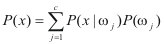
(for j possible states.)
|
|
