What does Bayes Decision Rule have to do with Pattern Recognition?
Let’s consider a three dimensional binary feature vector X=(x1,x2,x3) = (0,1,1) that we will attempt to classify with one of the following classes:

and lets say that the prior probability for class 1 is P(ω1)= 0.6 while for class 2 is P(ω2)= 0.4. Hence, it is already evident that there is a bias towards class 1.
Additionally, we know that likelihoods of each independent feature is given by p and q where:
pi = P(xi=1|ω1) and qi = P(xi=1|ω2)
meaning that we know the probability (or likelihood) of each independent feature given each class - these values are known and given:
p = {0.8, 0.2, 0.5} and q = {0.2, 0.5 , 0.9}
therefore, the discriminant function is g(x) = g1(x) - g2(x) or by taking the log of both sides:
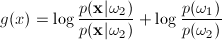
however, since the problem definition assumes that X is independent, the discriminant function can be calculated by:
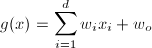
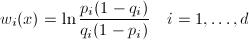
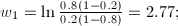
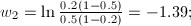
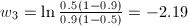
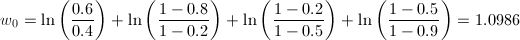

After inputting the xi values into the discriminant function, the answer g(x) = -2.4849. Therefore this belongs to class 2. Below is a plot of the decision boundary surface.
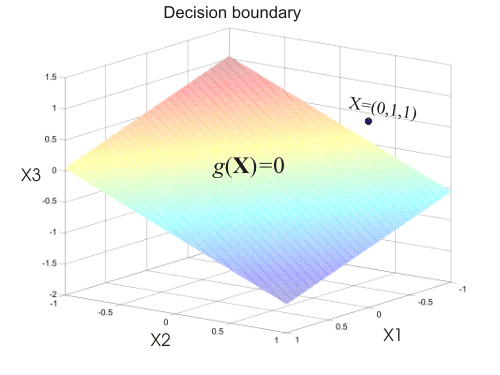
All points above the plane belong to class ω2 since if X = (0,1,1), g(x) = -2.4849 < 0.