An Introduction to Bayes Rule
To introduce Bayes rule and the theory behind it, consider the
following quote from a 2000
article in the Economist on the Bayesian Approach [link]:
"The essence of the Bayesian approach is
to provide a mathematical rule explaining how you
should change your existing beliefs in the light of new evidence. In
other words, it allows
scientists to combine new data with their existing knowledge or
expertise. The canonical example
is to imagine that a precocious newborn observes his first sunset, and
wonders whether the sun
will rise again or not. He assigns equal prior probabilities to both
possible outcomes, and
represents this by placing one white and one black marble into a bag.
The following day, when
the sun rises, the child places another white marble in the bag. The
probability that a marble
plucked randomly from the bag will be white (ie, the child's degree of
belief in future sunrises)
has thus gone from a half to two-thirds. After sunrise the next day,
the child adds another white
marble, and the probability (and thus the degree of belief) goes from
two-thirds to three-quarters. And so on. Gradually, the initial belief
that the sun is just as likely as not to rise each
morning is modified to become a near-certainty that the sun will always
rise."
Bayes
theorem is essentially an expression of conditional probabilities. More
or less, conditional
probabilities represent the probability of an event occurring given
evidence. To better
understand, Bayes Theorem can be derived from the joint probability of
A and B (i.e. P(A,B)) as
follows:
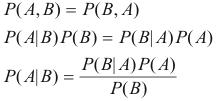
where
P(A|B) is referred to as the posterior;
P(B|A)
is known as the likelihood, P(A)
is the prior
and P(B)
is generally the evidence and is used as a scaling
factor. Therefore, it is handy to
remember Bayes Rule as:
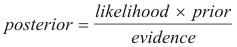
These
terms will be discussed a little later.
What does this all this mean? Well, to put this
into practical perspective observe the diagram below:
With Bayes Rule, it would be possible to determine
the probabiity that X belongs to either C1 or C2. Although in the above
example it is obvious that X is more likely to belong to C2 than C1,
the answer is usually not as clear. Bayes Rule helps determine this
probability, and Bayes Decision Rule helps make optimal decisions based
on this knowledge.

|
