Continuous Bayes Definitions
In the continuous realm, the convention for the probability will be as
follows:
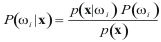
where x
is a feature vector in d-dimensional space |Rd
which will be referred to as feature space;
and ωj represent a
finite set of c possible states (or classes)
of existence: {ω1,
..., ωc}. Note the
difference in the above between the probability density
function p(x) whose integral
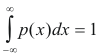
and a probability P(x)
represents a probability in the region of [0,1] in
which
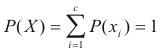 . .
As was stated earlier, the Bayes rule can be
thought of in the following (simplified) manner:
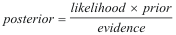
The Prior
As the name implies, the prior or a
priori distribution is a prior belief of how a particular
system
is modeled. For instance, the prior may be modeled with a Gaussian of
some estimated mean and
variance if previous evidence may suggest it be the case. Many times,
the prior may not be
known so a uniform distribution is first used to model the prior.
Subsequent trials will then yield
a much better estimate.
The Likelihood
The likelihood is simply the probability of
specific class given the random variable. This is
generally known and it’s complement is wanted - the a
posteriori or the posterior probability.
The Posterior
The posterior or a posteriori
probability (or distribution) is what results from the Bayes rule.
Specifically, it states the probability of an event occurring (or a
condition being true) given specific evidence. Hence the a
posteriori is shown as P(ω|x)
where ω is the particular query and x
is the evidence given.
The Evidence
The evidence p(x) is usually
considered a scaling term. Bayes Theorem also states that it is equal
to:
therefore, it is also possible to write:
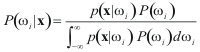
Independence and Conditional Independence
Briefly, it is important to discuss the terms of independence
and conditional independence since
they figure prominently in the Bayesian world. Independence essentially
ensures that two (or
more) random variables are not dependent on one another. Graphically,
this can be represtented
as:
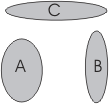
or mathematically by the Joint Probability: P(A,B,C)
= P(A)P(B)P(C).
Conditional independence is
more relevent to the Bayesian world however. It states that given
eveidence, one variable is independent of another. Hence if A ╨ B|C
(meaning A is independent of B given C) means that given evidence at C,
A is independent of B:

The conditional independence is
witnessed in the causal relationship above

|
