There are two main important points which we will investigate.
- Number of Flippable Edges : The
most important question to ask naturally arises to how many edges can be
flipped in given triangulation? Is there a bound? Using the
applet can you think of a general formula for the number of edges which can
be flipped?
We will show that there exists a tight bound on the number of edges which
can be flipped in a given point set and that similar results follow for
polygons.
The question is trivially for small point sets and polygons but consider
the following:
How many edges can be flipped in this polygon?
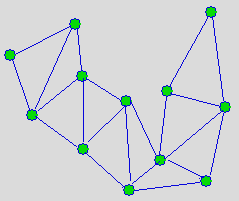
Is the question easy for the next triangulated
polygon?
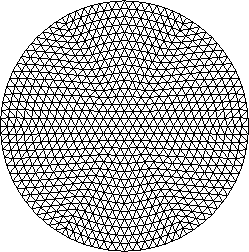
We note that the above
figure was taken from the site of the University
of Stuttgart.
- Diameter of Triangulations: That the bound on the diameter of the graph of triangulations of a point
set Pn that is sensitive to the number of convex layers of Pn.
What does the diameter of the graph of a triangulation show us? If
we define a graph of triangulations of a polygon Q to have a vertex set
corresponding to the triangulations of Q and an edge set defined of the set
of all adjacent vertices, with two vertices being adjacent if and only if
the triangulation corresponding to one vertex can be obtained from the
triangulation of the other corresponding endpoint by a single
flip.
| Look at the diameter of the polygon on the
left, AB. If our polygon represents the graph of a triangulations
of a polygon or point set. What can we say about the
diameter? The diameter gives us the maximum distance from any two
triangulations of a polygon. |
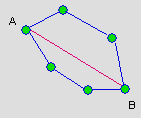 |

