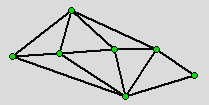
PRELIMINARIES

What is a triangulation of a Point Set?

Let P = {v₁,..., v_n} be a collection of points on the plane. 

A Triangulation of P is a partitioning of the convex hull of P, which we denote as CH(P), into a set of triangles T = {t₁,...,t_m}.

 Each triangle of T has a disjoint interior such that the vertices of each triangle t₁ of T are points of P.  Further, the elements of P are called the vertices of T and the edges of the triangles t₁,...,t_m of T are called the edges of T. 

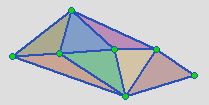
The degree of a vertex v, which we denote as d(v) is the number of edges of T that have v as an endpoint.

Flipping the edges of a triangulation

An edge of T is flippable if e is contained in the boundary of two triangles t and t' of T and C = tUt' is a convex quadrilateral. We define flipping e to mean the operation of removing e from T and replacing it by the other diagonal of C.

Describing a triangulation using a graph

Given a collection of points P_n = {v₁,..., v_n} we define the graph G_T(P), the graph of triangulations of P_n, to be the graph such that the vertices of G_T(P) are the triangulations of P, two triangulations being adjacent if one can be obtained from the other by flipping an edge.

Distance between triangulations

Given two triangulations T' and T'' of P, we can say that they are at distance k if their distance in G_T(P) is k. Stated another way, that means there is a set of k triangulations T_o = T',...,T_k = T'' such that T_i+1 can be obtained from T_i by flipping one edge, for all i = 0,..., k-1. 

We also say that T' can be transformed into T'' be flipping k edges.

Triangulations and Edge Flipping of Polygons

Triangulations of polygons, flipping edges in them, and their corresponding graphs of triangulations are defined in an analogous way.

Assumptions for proofs and theorems

Make note of the following notations and assumptions! 

We denote point sets as P_n and polygons as Q_n. The vertices of Q_n are assumed to be labeled in clockwise order and that no three consecutive vertices are collinear.

Notice the clockwise labeling of the vertices of polygon on the left!

ABCD are collinear! We are not going to consider polygons of this type!

We denote the graph of a triangulation of a point set P as G_T(P) and similarly for a polygon Q, G_T(Q).

We denote the convex hull of a point set P as CH(P).