Flipping Edged in Triangulations

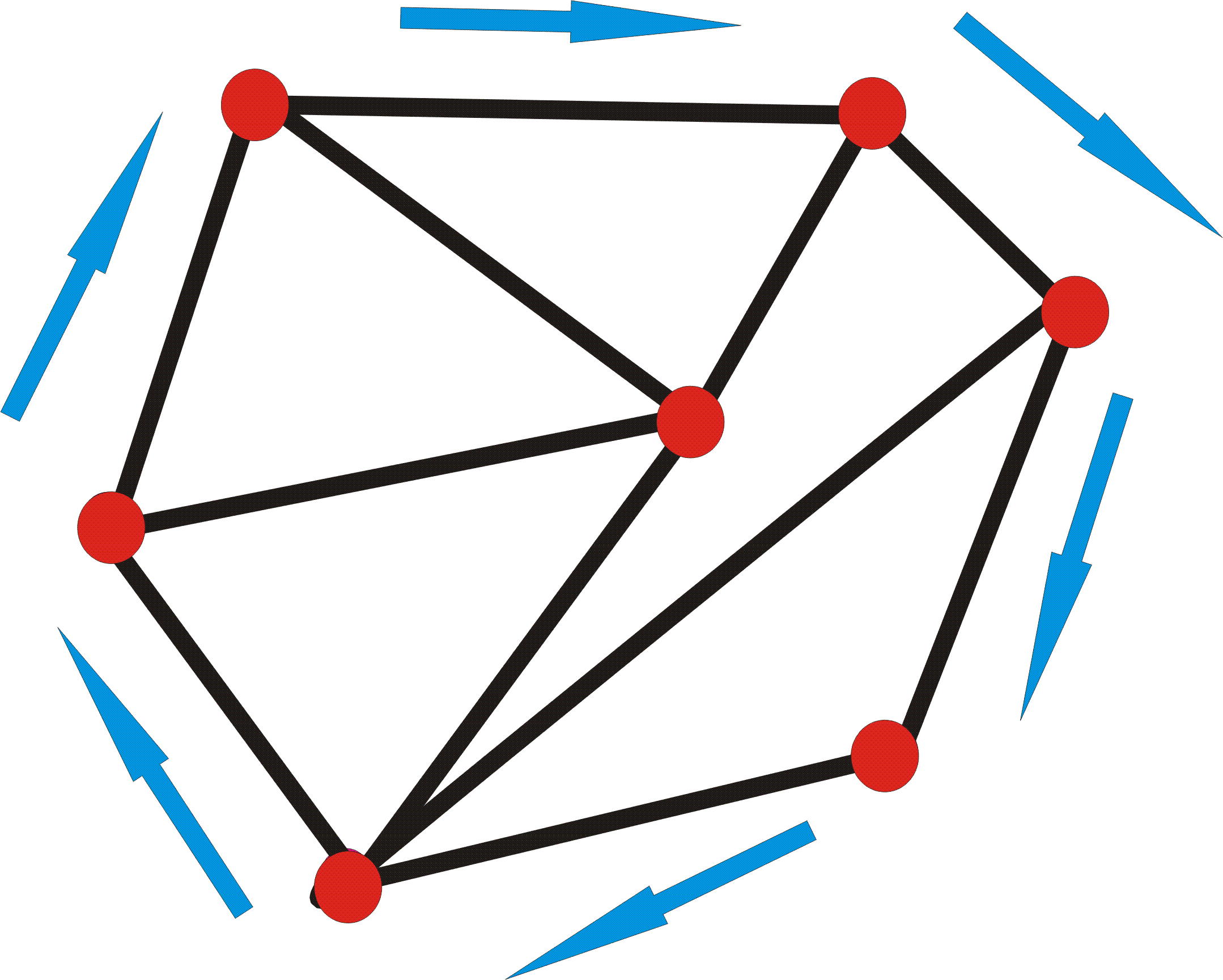
NUMBER OF FLIPPABLE EDGES

Given a triangulation T of a collection P_n = {v₁,...,v_n} of n points on the plane, how many edges of T are flippable?

The following theorem gives us the result. You can intuitively see the result by trying different triangulations in the applet.

Theorem 1:

Any triangulation of a collection of P_n of n points on the plane in general position contains at least ceiling[(n-4)/2] flippable edges.

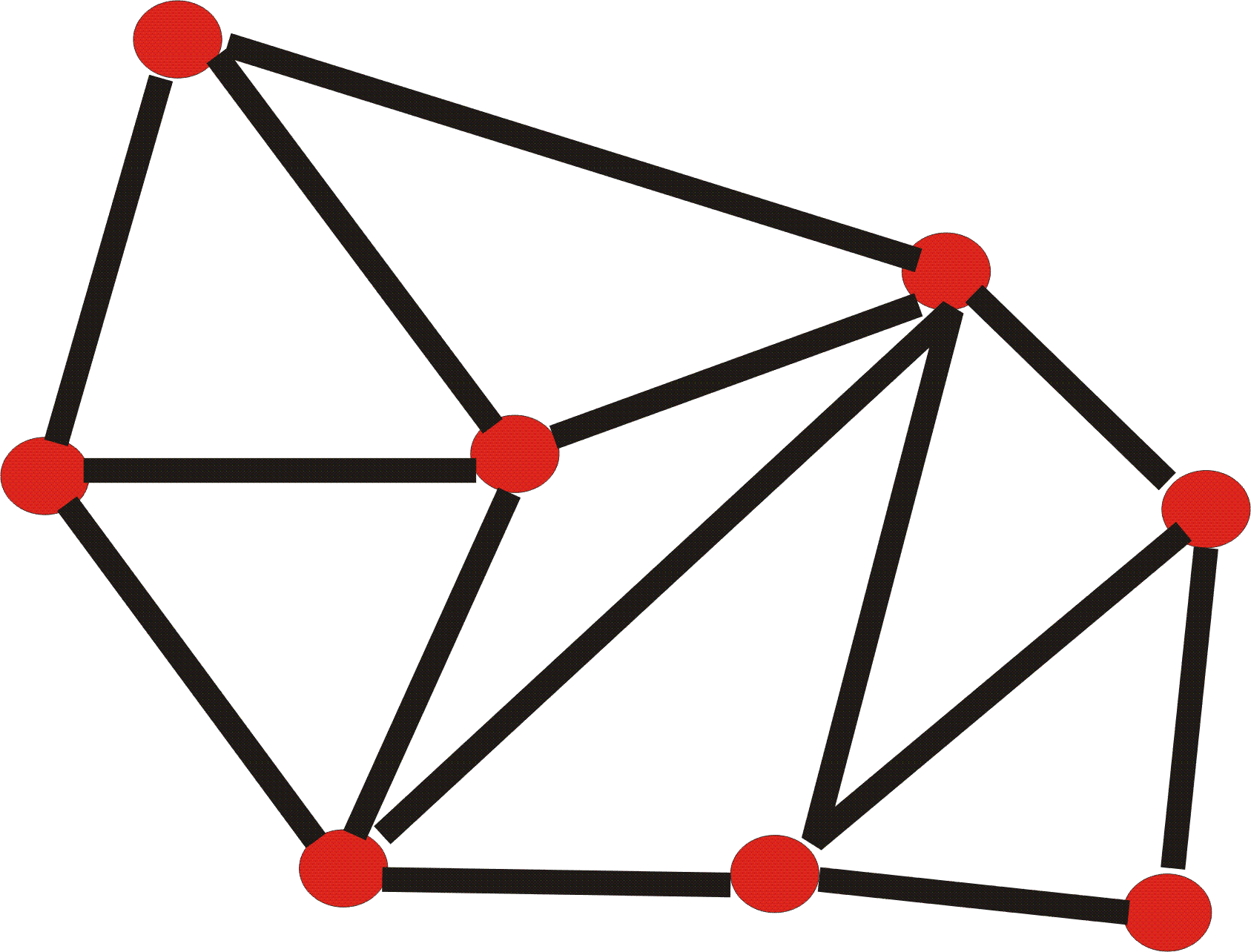
We will come back to the proof of Theorem 1 after investigating the problem further....

The above figure show a triangulation of a point set where only (n-2)/4 edges are flippable

General Position Assumption

It is important to note that the general position assumption is necessary since otherwise it is easy to construct a triangulation where no edge can be flipped.


If we do not assume that no three points can be collinear then we must take polygons such as above in account. Above: n-3 points in one of the sides of a triangle of a polygon with n points.		We can see that if we have such a case than there exists a subset of edges which are not flippable because they are collinear. In our example there are no flippable edges!

Further notation

Given a triangulation T we can divide the set of edges of T into two subsets:

F(T) which contains all flippable edges of T;
NF(T) which contains all not flippable edges of T.

Clearly all the edges of T contained in the boundary of the convex hull of P_n are not flippable.

We create an orientation of each edge e in NF(T) as follows:

RULE 1: If e is an edge of CH(P_n), orient it in the clockwise direction around CH(P_n) of P_n.

Rule 1: The following shows the orientation when the nonflippable edges are oriented around the convex hull.

RULE 2: If e=uv is not in CH(P_n), consider the quadrilateral C formed by the union of the two triangles of T containing e. Since C is not convex, it follows that one of the end vertices of e, say v, is a reflex vertex of C while u is a convex vertex of C. Orient e from u to v. We observe that the angle of C at v is greater than 180 degrees.

Rule 2: The following shows the orientation when the nonflippable edges are not convex hull edges.

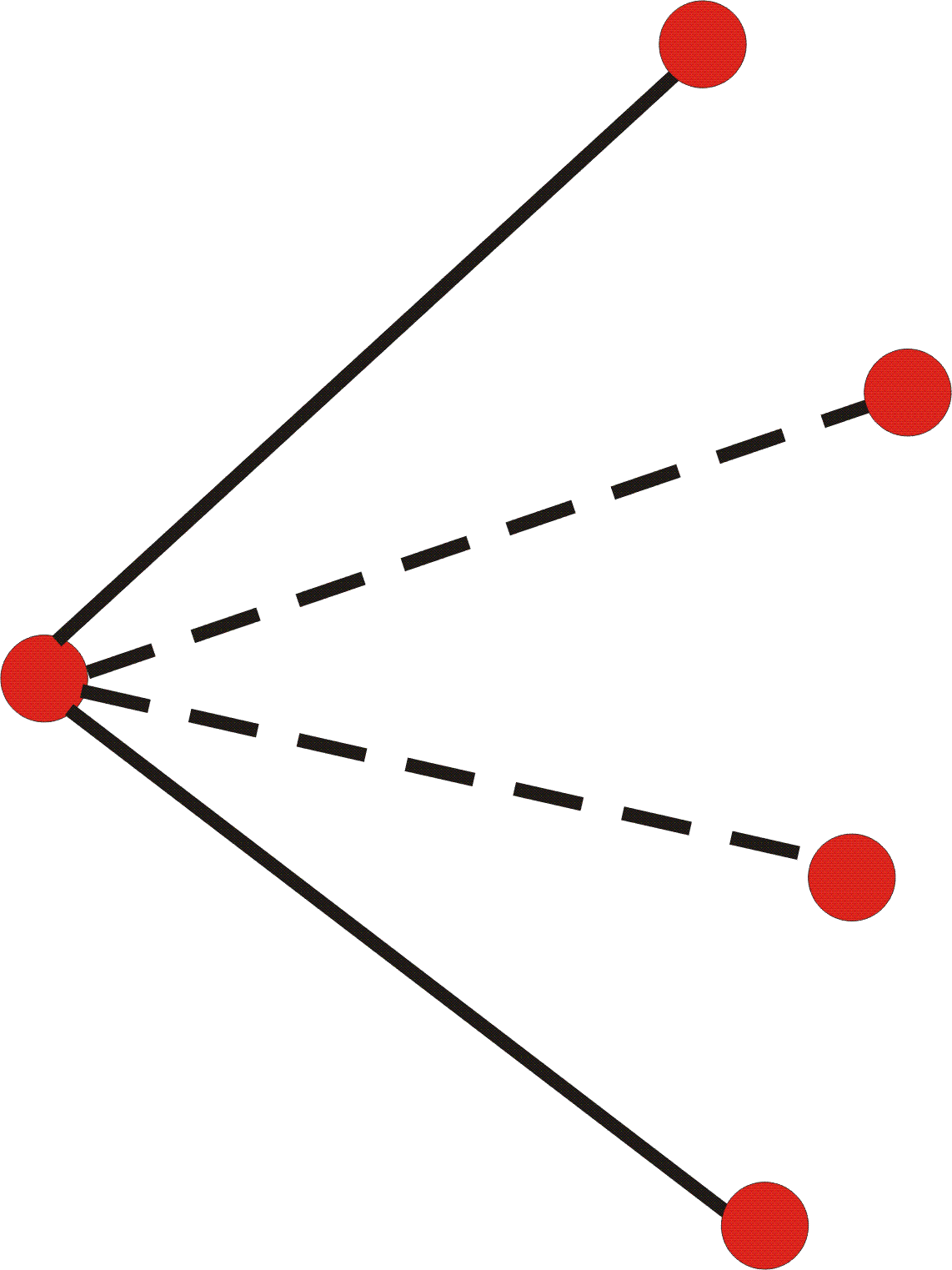
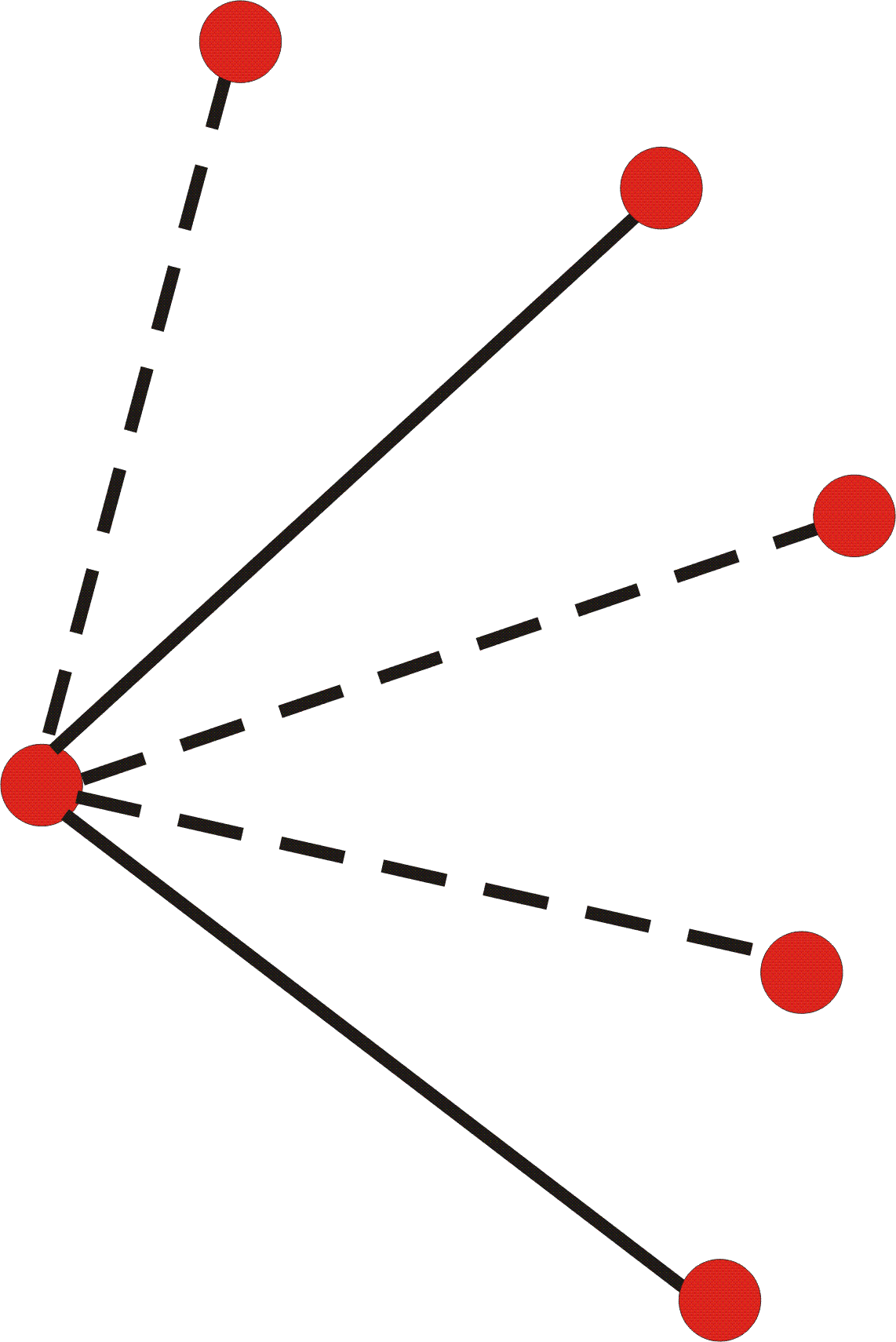
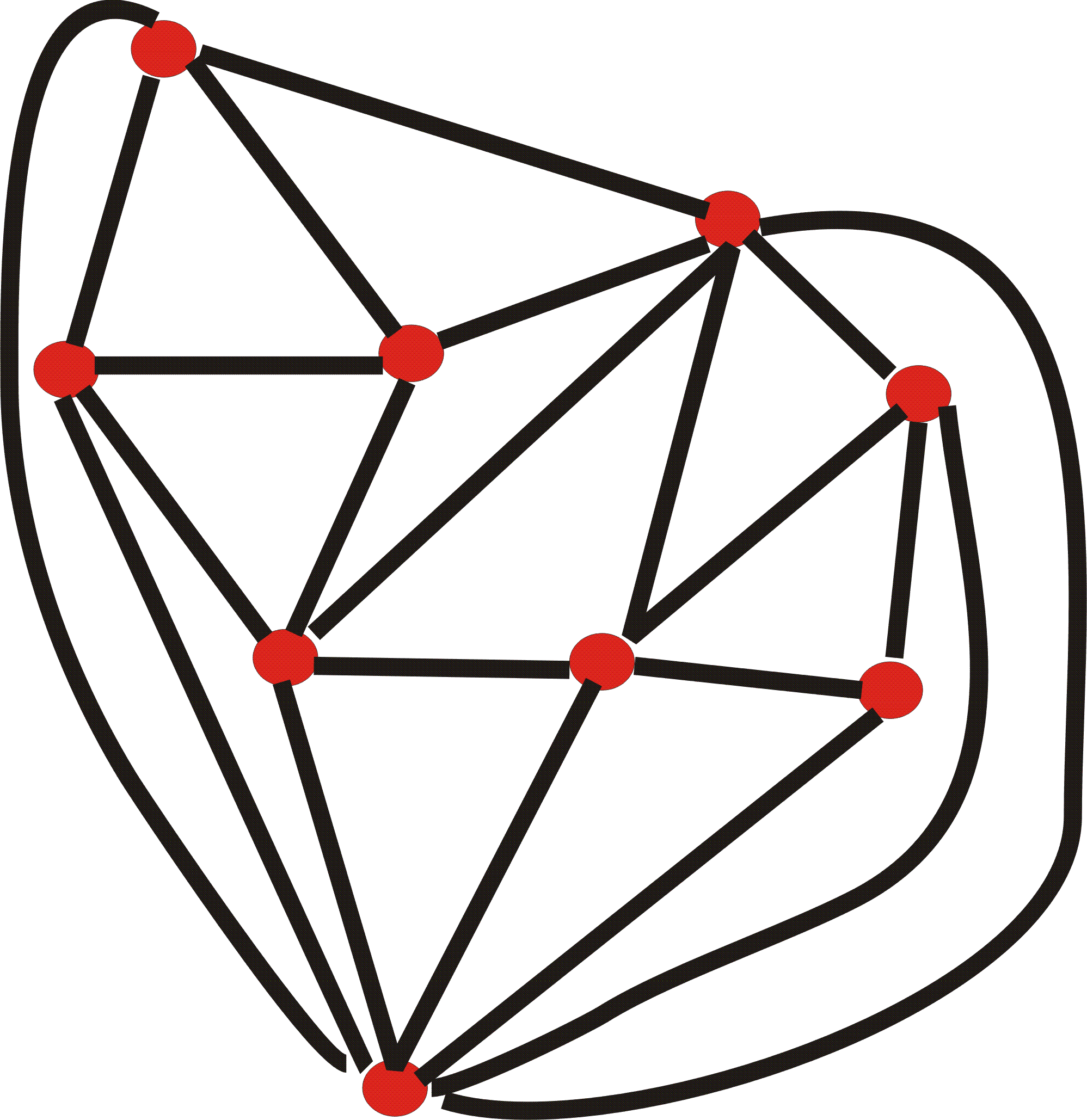
Consider any vertex v_i of T. Let d^-(v_i) be the number of edges of v_i in NF(T) oriented from v_j to v_i. Note that d(v_i) is the total number of edges of T incident with v_i, whereas d^-(v_i) involves only edges of T in NF(T).

Helpful Lemma

We use the following lemma to prove our main theorem...

Lemma 2:

Let v_i be any vertex of T. Then d^-(v_i) ≤ 3. Moreover, if d(v_i) > 3 in T, then d^-(v_i) ≤ 2. If d^-(v_i) = 2, the edges oriented toward v_i are consecutive edges around v_i.

Proof of Lemma 2:

If v_i is in CH(P_n) then d^-(v_i) = 1. Next, suppose then that v_i is in the interior of CH(P_n); then two cases arise:

Case 1: d(v_i) = 3 in T. In this case, all the edges of T incident with v_i are nonflippable and are oriented toward v_i. It follows that d^-(v_i) = 3.

Case 2: d(v_i) > 3 in T. It is obvious that no more than two edges of G can be oriented toward dv_i and that if d^-(v_i) = 2, then the two edges oriented toward v_i must be consecutive edges incident to v_i.

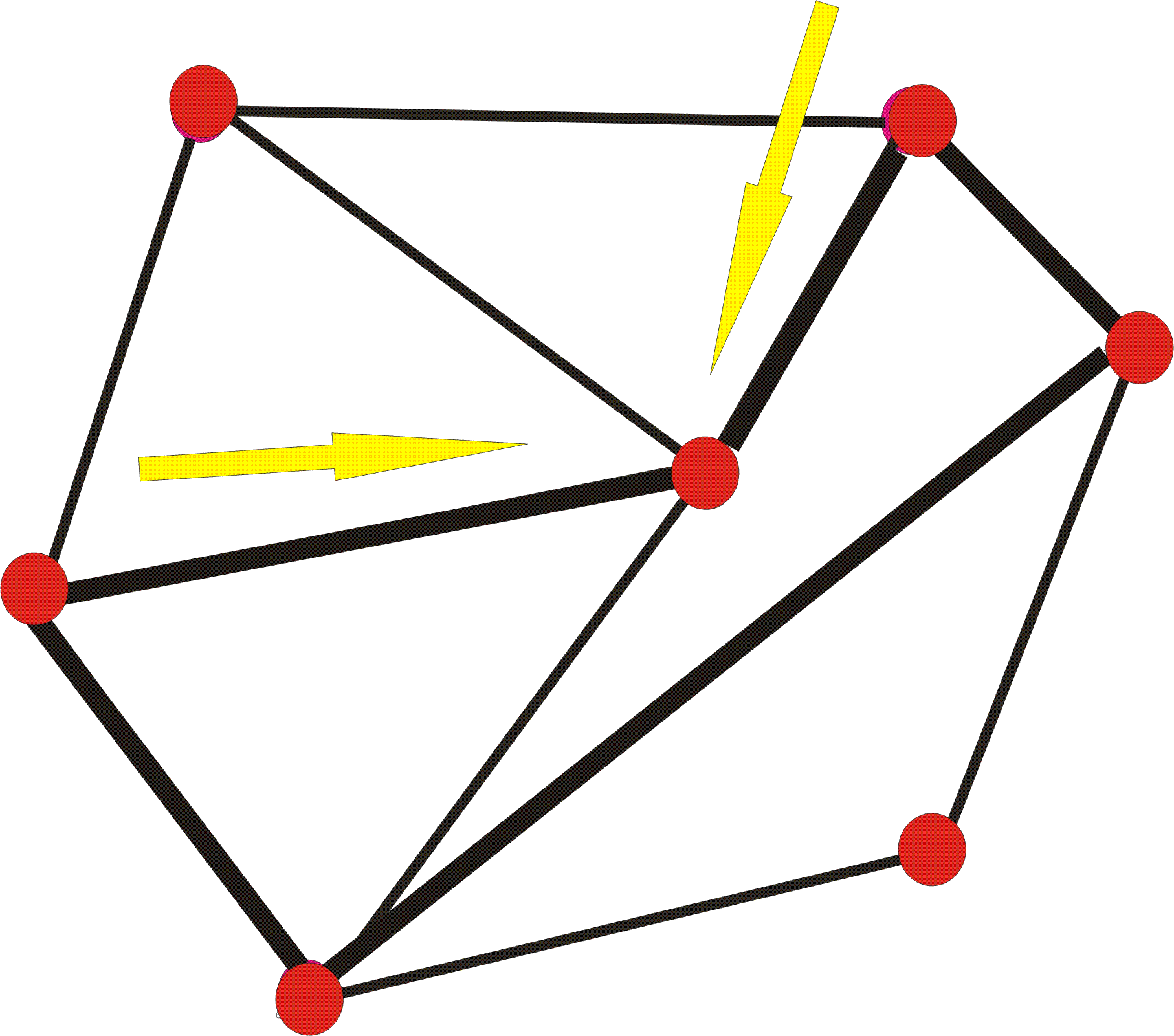
In the Below figured the oriented, nonflippable edges are the dashed lines whereas the flippable edges are solid.

On the left the leftmost vertex has total degree 4 and 2 nonflippable edges. Thus, the edges are consecutive.

On the right vertex does not have valid degree. The total degree is 5 but the number of nonflippable edges is 3. From lemma 2, this is not valid.

Main Theorem

Using Lemma 2 and the above information we can now go on to prove Theorem 1.

Proof of Theorem 1:

The proof comes in the following steps:

Step 1: Start with initial set of points and find a triangulation of the points.

Let P_n be a set of points in general position on the plane (see below)

let T be a triangulation of P_n (see below)

In our triangulation we let S be the set of elements of P_n with degree 3 in T that are not in CH(P_n).

Step 3: Add an auxiliary point and join it to each of the points on the convex hull of our triangulation.

We add a point w exterior to CH(P_n) and join it with a set of disjoint edges to all the vertices in CH(P_n). By this we obtain a triangulation of the plane with n+1 points which by Euler's theorem contains 3n-3 edges.

Above we see that the point w added is the bottom most point.

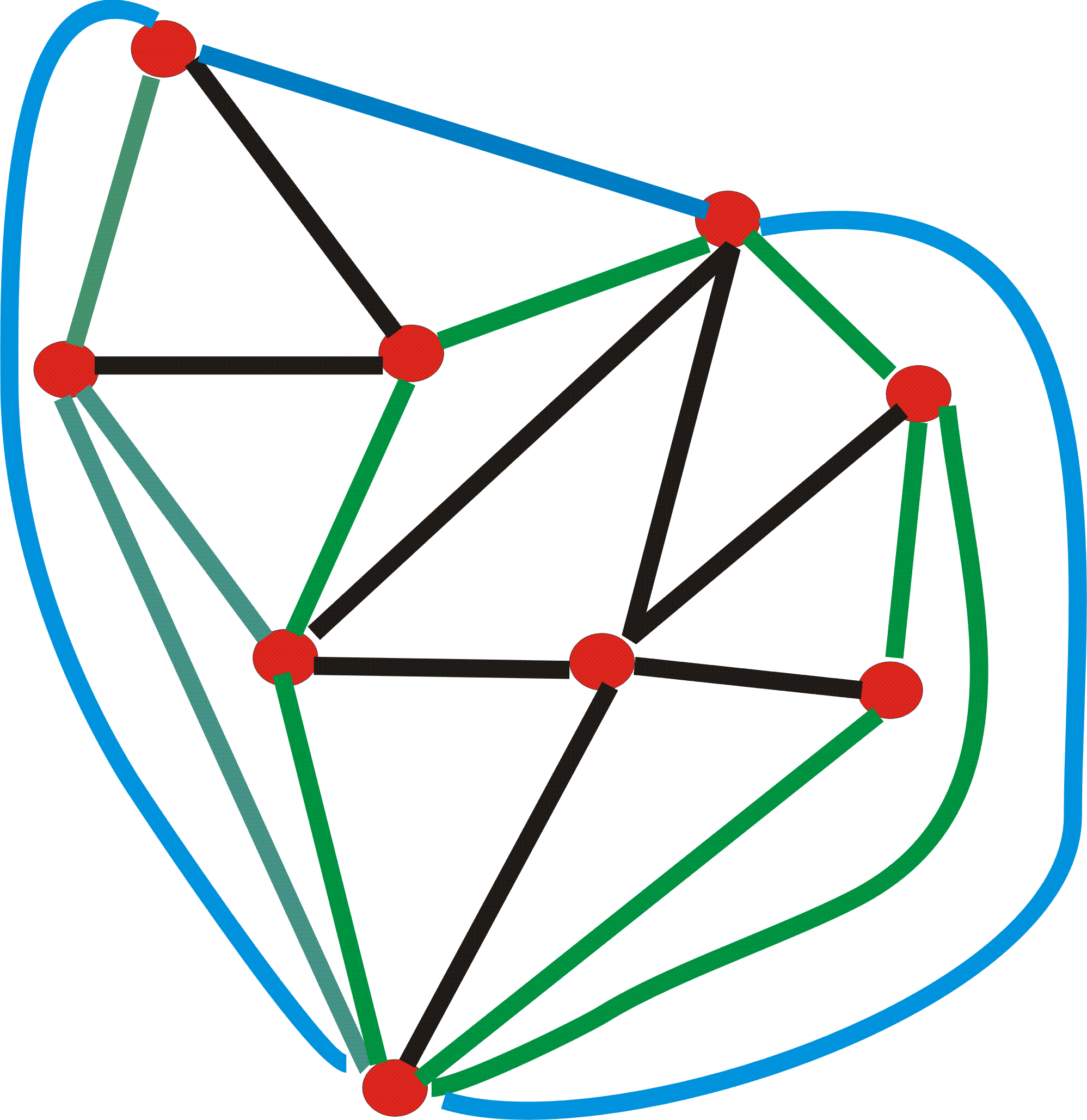
Step 5: Orient the edges according to Rule 1 and 2.

Each of the edges incident to w are contained in NF(T) and we orient them from w to the vertex contained on CH(P_n). Next we orient all edges of T in NF(T) according to Rule 1 and Rule 2 above (see below). Notice that with these orientations, d^-(v_i) = 2 for all the elements of P_n of CH(P_n).

The edges oriented using Rule 1 are blue and the edges oriented using rule 2 are in green.

Step 6: Remove all the vertices in the set S.

Next we remove from T all the elements of S. Notice that we remove exactly 3|S| edges of T which are not flippable and what remains is a triangulation T' of P_n - S + {w}, which by Euler's formula contains 2(|P_n - S| + 1) - 4 = 2(n - |S|) - 2 triangles. Any element v_i of P_n - S + {w} that is not in the convex hull of vertices of P_n - S + {w} that have d^-(v_i) = 2.

Step 7: Use lemma 2 on the resulting graph of step 6.

Using lemma 2 we can associate to every vertex v_i of Q in the interior of CH(P_n) a triangle t(v_i) of T' which is also a triangle in T, bounded by two oriented edges and the triangles t(v_i) are all different. To each vertex v_i of T' in CH(P_n) we can also associate a different triangle of T' among those having w as one of their vertices. Therefore, to each vertex of T' which is not w or a vertex of T' with d^-(v_i) < 2, we associate a different triangle of T' that contains no element of S. Thus, the number of edges of T that can be flipped is minimized when all the vertices v_i not in S have d^-(v_i) = 2. We have n - |S| triangles associated with vertices in Q and as T' has 2n - 2|S| - 2 triangles, at most n - |S| - 2 of them contained points of S in T. Using the inequality |S| ≤ n - |S| - 2 we get:

(3n - 3) - 3|S| - 2(n - |S|) = n - |S| - 3 ≥ (n - 4)/2

which is the number of flippable edges in T.

Analogous Results for Polygons

We have analogous result of Theorem 1 for polygons.

Theorem 3:

Any triangulation of a polygon Q_n with n vertices, k of them being reflex, contains at least n - 3 - 2k diagonals that can be flipped.

Last Updated December 2, 2003
By Christina Boucher
cboucher@geeky.net