|
|
Flipping Edged in Triangulations |
|
GLOSSARYConvex Angle: An internal angle which is less than 180 degrees. Convex Hull: The convex hull of a set of points is the smallest convex set that includes the points. The site Convex Hull Algorithms by Tim Lambert gives an excellent tutorial which demonstrates algorithms for computing the convex hull in 3 dimensions.
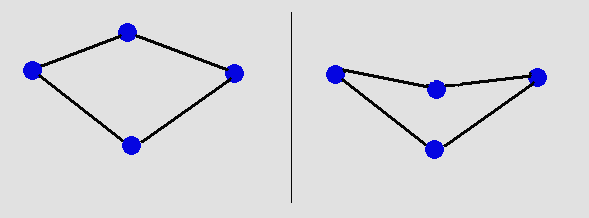
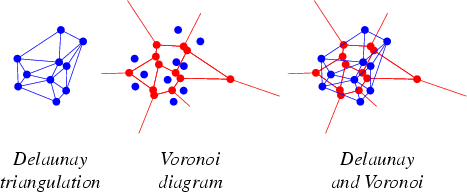
Convex Quadrilateral: a quadrilateral whose angles are all less than 180 degrees. We have a convex quadrilateral on the left and a non-convex quadrilateral on the right. Degree of a Vertex : the degree of a vertex v is the number of edges which have v as an endpoint.Delaunay triangulation: For a set Pn of points the plane the unique delaunay triangulation, denoted as DT(Pn ), is the triangulation such that no point in Pn is inside the the circumcircle of any triangle of DT(Pn ). DT(Pn ) is the dual of the voronoi diagram of Pn. The figure showing delaunay triangulation was taken from mathworld.wolfram.com.
Diameter: the diameter of a polygon is defined as the maximum distance between any two points of the polygon. Dual Graph: Given a planar graph G, its geometric dual G* is constructed by placing a vertex in each region of G (including the exterior region) and if two regions have a edge x in common, joining the corresponding vertices by placing an edge x* crossing only x. Edge Flipping: We define flipping an edge e to mean the operation of removing e from T and replacing it by the other diagonal of the convex quadrilateral containing the adjacent triangles. Euler's theorem: For any convex polyhedron, the number of vertices and faces together is exactly two more than the number of edges. Symbolically V-E+F=2, where V denotes the vertices, E denotes the edges, and F denotes the faces. For instance, a tetrahedron has four vertices, four faces, and six edges; 4-6+4=2. Reflex Angle: An internal angle which is greater than or equal to 180 degrees. Triangulation: A triangulation of Pn is a partitioning of CH(Pn) into a set of triangles T with disjoint interiors, such that the vertices of each triangle T are points of Pn. See figure for delaunay triangulation. Spiral Polygon: A polygon Qn is called a spiral polygon if the vertices of Qn can be labeled v1,..., vs,vs+1,...,vn such that v1,...,vs are reflex vertices of Qn and vs+1,...,vn are convex vertices of Qn. Voronoi Diagram: The partitioning of a plane with a set of n points Pn into n convex polygons such that each polygon contains exactly one point and every point in a given polygon is closer to its central point than to any other. See figure for delaunay triangulation. |
|
|
Last Updated
December 2, 2003 |