|
|
Suppose we have one set of blue dots and another one of red dots
(see figure 1). Suppose also that we have another dot that we are trying to
determine whether it should be colored red or blue. To decide about its color
we measure the shortest distance between this dot to the other red or blue
dots. We decide to color the dot with the color of its closest neighbor.
Figure 1 Shortest distance to red dot is less than the shortest
distance to blue dot
Figure 1.1 identification of the shortest distance to the new
dot.
Figure 1.2 determination of the color of the new dot to red. Hence we just defined the Nearest Neighbor [1] learning
Algorithm introduced in the 1950s with two classes( red and blue dots). This
algorithm was applied to diverse fields: Artificial intelligence, pattern
recognition…etc. some researchers have found that the NN (nearest neighbor)
classifiers have bounds on their error rate. The basic NN algorithm is
summarized as follows. An example is a vector of real numbers plus a label
that represents the name of a category. Assuming a domain with n features,
where all features have been normalized to the same range, the distance
between two examples X=(x E (X,Y)= The NN algorithm is simple: 1. Store
all training instances, plus their classifications. 2. For
a new example X, compute the distance between X and each stored instance. 3. Let
A be the stored instance of the minimum distance to X. Output the
classification of A as the predicted classification of X. Many researchers worked on the bounds on the error rate that NN
classifiers obtain. I will discuss about the best-case bounds. Our objective is to find the best-case bound for the NN
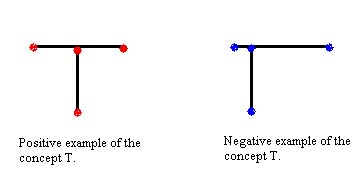
classifier. In the example of the letter T presented below the label is the
letter T. Example of an automated handwriting recognition system based on the
NN algorithm that must be trained by the user. Consider the problem of
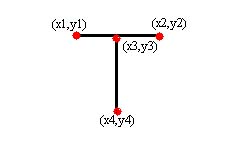
training the system to recognize the letter T. we can described T by eight
features: the endpoints of the horizontal line segment (x1, y1) and (x2, y2)
and the endpoints of the vertical line segment (x3, y3) and (x4, y4). The
definition of the character T can be expressed by:
where e1,e2,e3 and e4 tends to zero. These inequalities are also
called a concept describing the letter T (figure 2).
Figure.2 (concept of the letter T) Another way to represent this concept is as a geometric
region in
Figure 2.1 |