|
Description
of the Best-Case Model
A learning algorithm (NN learning for example) takes a
training set S of examples:
S = {X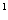 , X , X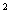 ,..., X ,..., X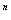 }, },
where each example consists of a set of d features plus a
category label. The algorithm must use the examples to build a representation
with which it will classify a test set T of new examples.
A concept is a mapping from the set
of all examples in a domain to a set of labels. A concept class is a set of
concepts.
For example, in the domain defined by
the unit square, the partitioning defined by the line x=0.5 might be a
concept where any (x,y) in which x<=0.5 is labeled 0, and x>0.5 is
labeled 1. An example of a concept class in this domain might be the set of
all partitioning defined by lines of the form x=r, where 0<=x<=1. If
the examples si are contained in Rd, then an equivalent term for concept is
decision boundary, where the boundary includes all surfaces separating the
classes.
We will say that a learner has
learned a concept exactly if it correctly classifies all possible examples.
The distribution from which the new examples in T are taken can be
different from the distribution used for S. because our model is not
statistical; the results are independent of any assumptions about these
distributions.
In the best-case
model, the learning algorithm and the concept are fixed and known to the
teacher. The teacher then chooses examples for S in the best way possible.
"best" means the learning algorithm requires a minimum number of
training examples to learn a concept. The term sample complexity refers to
the number of examples required for learning. The teacher is able to
compute a representation of the concept in the same language used by the
learner.
Even when using the best-case model,
some concept classes still have exponential sample complexity for the NN
algorithm.
|