EXAMPLE OF PROBLEMS:

Theorem1: A simple polygon may be convexified with O(n2) reversals while maintaining simplicity after each reversal.

Theorem2: A star-shaped polygon can be convexified with O(n2) edge-swaps while maintaining star-shapedness after each edge-swap, and bound is tight in the worst case.
For Proof [2]

Theorem3: Determining whether a signed polygon may be permutated using transpositions so that its shape is rotated by an angle of 180 takes Teta(nlogn) time in the algebraic decision tree model of computation.
For Proof [2]

Theorem4: Determining whether we can obtain the mirror image of a signed polygon using transpositions takes Teta(nlogn) time in the algebraic decision tree model of computation.
For Proof [2]

 

   "The purpose of studying the complexity of convexifying a polygon by means of permutations, is precisely because we can easily model a polygon from another polygon by going through it's convex form and thus for example getting the complexity of mutating the genome of a mouse into the genome of a human being."

PROOF OF THEOREM1: [1]

This result holds for the more restricted reversal operation of Filpturns. Therefore, I will prove that any simple polygon with n vertices will be convexified after any sequence of at most n(n-3) Flipturns, and more generally (n(s - 1)/2) - s Flipturns with s being the number of different edges slopes in the polygon.

Fig of Flipturns:

           

 

First we will define Flipturns:

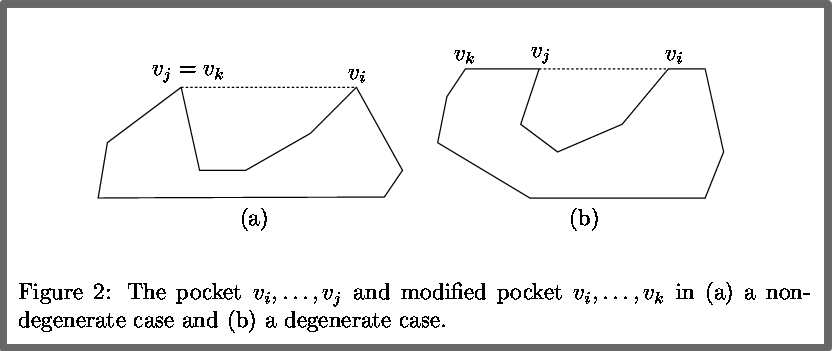
- A pocket p=(vi, …. , vj) of a simple polygon P is a subchain of P such that vi and vj are on the convex hull of P an all the vk suck that i<k<j are not on the convex hull of P.

- A lid l(vi,vj) is the line segment joining the two endpoint of a pocket.

- A Flipturn is a rotation of a pocket p=(vi,…. , vj) by 180 degrees about the midpoint of the lid l(vi,vj).

 

 

 

 

And now some notations:

- dir(ei):  The direction of an edge ei of P.

- The set of all directions and their negations used by edges of P.

- (with m being the number of directions): one plus the number of other directions in S between di and dj as we rotate di in the counterclockwise direction.

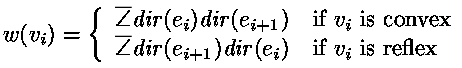
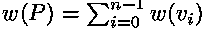
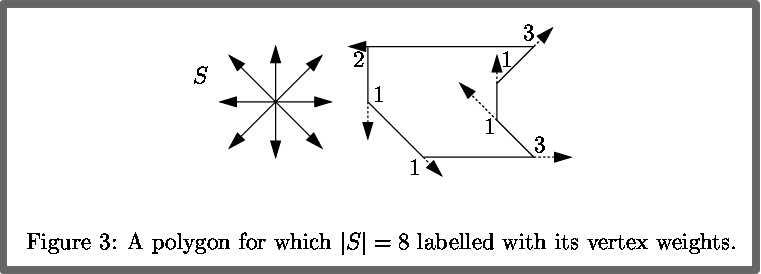
s = |S/2|.

Observations:

w(vi) <= s-1 which implies that w(P) <= n(s-1)

 

Assumption we wont prove:

LEMMA1:  For any convex polygon P, we have w(P) = 2s

LEMMA2:  r + b - r’ - b’ >= 2.

Let r and b be the weight of vi and vj, respectively, before performing a flipturn and let r’ and b’ be the weight of the vi and vj, respectively, after performing the flipturn.

Therefore, since the weight of P is at most n(s - 1) [according to the observations] and once convexified it will be 2s [according to LEMMA1]. Also LEMMA2 says that the weight of P decreases by at least 2 after every flipturn:

Therfore
Let F be the number of Flipturns

n(s - 1) - 2F = 2s
2F = n(s - 1) - 2s
  F = n(s - 1)/ 2 - s

End Of Proof

 

If we take s as been equal to n [n edges => n different edge slopes], the number of Filpturns is O(n2)