In order to simplify the exposition of the permutation problem, we will only look at signed simple polygons.
Given a signed simple planar polygon with a sequence of edges e = {e1, e2, ...., en} we examine the effects of several operations that permute this sequence, resulting in the formation of a new polygon. The purpose is to study the complexity of performing certain actions such as convexifying a given polygon or obtaining the mirror image by using these permuting operations.
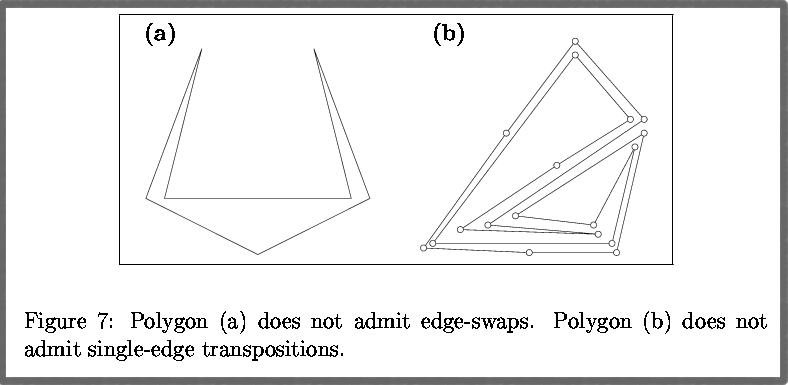
Some form of restrictions must be imposed upon those operations so that we do not deteriorate the goals of this research. One of which is the conservation of simplicity. In other words applying a permutation on a simple polygon must produce another simple polygon, therefore some polygons do not admit certain type of operations. Here an example:

Polygon that do not admit any edge-swaps.

 

 

 

 

There's 3 main operations that we can consider:

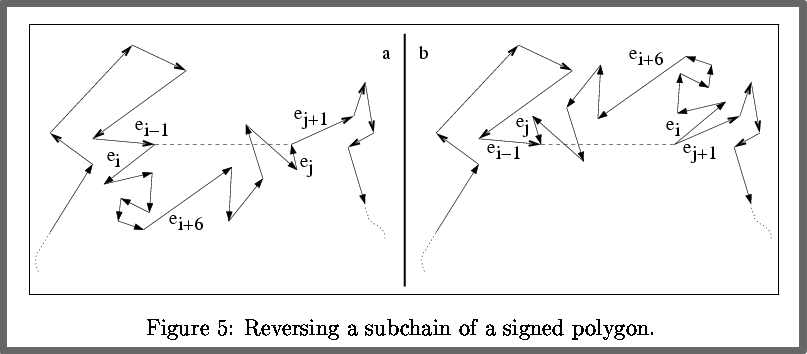
Reversal:   Inverting the order of a subsequence

* Geometrically equivalent to rotating the subsequence rigidly in the plane by an angle of 180 so that its endpoints are placed exactly at each other’s original location.

* A more restricted class of reversals is called Filpturns. We are going to use Filpturns later in order to prove an upperbound on the number of reversals required to convexify any simple polygon.

 

 

 

 

 

 

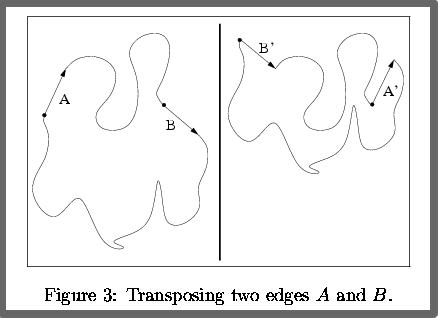
Transposition: Interchanging the edges between two subsequences (no edge sharing allowed).

* Conserves the orientation of a signed polygon

 

                                                  

 

 

 

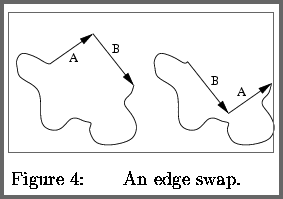
Edge-Swap: Special case of a Transposition, it consist of interchanging two consecutive edges.

* Conserves the orientation of a signed polygon