New Page 2

____________________________________________________________________________________

Preliminary

Area of a triangle

From linear algebra, we know that the magnitude of the cross product of two vectors is the area of the parallelogram they determine: let a(x_a, y_a ), b(x_b, y_b ), c(x_c, y_c ) are three vertices of a triangle T, see Figure 10, let us denote this area as A(T)

Fig.10

2A(T) = (x_Ay_B - y_Ax_B ) (1)

where A=b-a, B=c-a, so we have:

2A(T) = 2A(a, b, c) =x_ay_b - y_ax_b+y_ax_c - x_ay_c+x_by_c - x_cy_b (2)

Area of a convex quadrilateral

The area of a convex quadrilateral Q=(a, b, c, d) can be written in two ways, depending on the two different triangulations (see Fig.11)

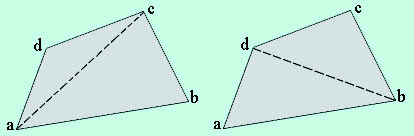
Fig.11

A(Q) = A(a, b, c) + A(a, c, d) = A(d, a, b) + A(d, b, c)

2A(Q) = x_ay_b - y_ax_b+y_ax_c - x_ay_c+x_by_c - x_cy_b

+x_ay_c - y_ax_c+y_ax_d - x_ay_d+x_cy_d - x_dy_c

Note that the terms y_ax_c - x_ay_c apear in A(a, b, c) and in A(a, c, d) with opposite signs and so cancel, that means the diagonal ac cancel. Thus the exact expression of A(t) is independent of the triangulation.

Area of a nonconvex quadrilateral

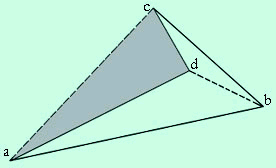
Fig.12

See Figure 12. even though the diagonal ac is external to Q, the algebraic expression is still independent of the diagonal chosen, the equation:

A(Q) = A(a, b, c) + A(a, c, d)

Because note that (a.c.d) is a clockwise path, so the cross product for the area will be negative, i.e. A(a, c, d)is negative, and is therefore subtracted from the surrounding triangle (a, b, c).

Area from an arbitrary Center

Let us generalize the method of summing the areas of the triangles in a triangulation to summing areas based on an arbitrary, external, point p. Let T=(a, b, c) be a triangle with the vertices oriented counterclockwise, p is any points in plane

A(T) = A(p, a, b) + A(p, b, c) + A(p, c, a)

It is easy to know that A(p, a, b) is negative because clockwise. and A(T) is independent of point P(see Fig.13)

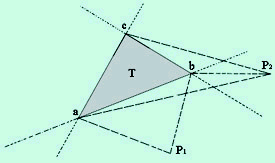
Fig.13

So we may generalize the result for arbitrary polygons.

Lemma: let a polygon (convex or simple) P have vertices v₀,..., v_n-1 labeled counterclockwise, let p be any point in plane, then

A(P) = A(p,v₀, v₁) + A(p,v₁, v₂)+ ...+ A(p,v_n-2, v_n-1) + A(p,v_n-1, v₀)

where v_i =( x_i, y_i), it can be seen as vectors from the origin. Here the method is known as the polar formula.

__________________________________________________________________________________