| Main Page | Introduction | History | Preliminary | Algorithms | Applet | References |
____________________________________________________________________________________
Introduction
The measure of areas of sets is fundamental problem in mathematical and Computational Geometry. It is straightforward to see that calculating areas of polygons in the plane can be done in linear time, even for the following problems:
Suppose that we split a simple polygon P into two subpolygons P1 and P2 by cutting it along a line segment joining two mutually visible points s and t on its boundary, see Figure 1,
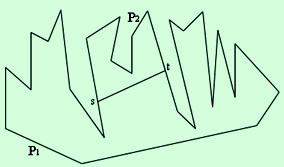
Fig. 1
can be solved optimally in linear time. But how quickly can we measure the areas of P1 and P2? So our solution here, is to present a simple and practical data structure for storing the partial sum's areas, so that after linear amount of preprocessing, P1 can be gotten in constant time.
Given 2n rays from one point, for a query line l crossing all 2n rays, how can quickly return the sum of the areas of the n triangles Ai bounded by l and the lines 2i-1 and 2i (see Figure.2 )? Here in this project the solution is given by using FFT (Fast Fourier Transform).
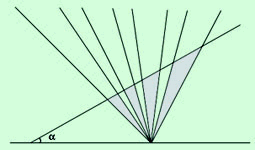
__________________________________________________________________________________
| Main Page | Introduction | History | Preliminary | Algorithms | Applet | References |