New Page 2

____________________________________________________________________________________

Algorithms

Problem 1: let P={v₀,..., v_n-1} be a convex polygon, preprocess P so that for a query line of P we can quickly determine the pieces of P.

Algorithm 1 Preprocessing convex polygons

Let T_v0 be the triangulation of P given by joining v₀ with all other vertices of P. Let T_i be the triangle with vertices{v₀,v_i,v_i+1} and let R_i be its area, for i=1,...,n-2.
Let A₀=0,A₁=0,A₂=R₁,A_i=R₁+...+R_i-1,for i=3,...,n-1(see Fig.14).

Fig.14

The intersection points p and q of a line with the boundary of a convex polygon can be found in logarithmic time (see [PS85]). For example, in Fig.14 let P₁ be the polygon including vertices v₀,p,q, AT(pq) be the area of subpolygon with vertices v₀,v₃,p,q,v₇,so the area of P₁:

A(P₁)=A₄ + AT(pq) + A₁₀ - A₈

can be calculated in constant time, we have:

Theorem 1 : Given a convex polygon P with n vertices, after O(n) preprocessing time, the pieces of a convex polygon split by a line can be in O(logn) time

__________________________________________________________________________________

Problem 2: let P={v₀,..., v_n-1} be a simple polygon, preprocess P so that for a query chord t of P we can quickly determine the area of P_t.

For any line segment t with the endpoints a and b, we denote A(t)=x_ay_b - y_ax_b and equals twice the area of the triangle whose vertices are the origin and the endpoints of t.

Let A(P) be the area of P and let e₁ ,....e_n be the edges of P in counterclockwise:

Now use the idea of partial sums, for each edge e_k, we store:

Suppose that chord t has its endpoints on the edges e_j and e_k,j<k-1. Let A( t' ) be the sum of the area of:

A( t' )=A(v_j-1a) + A(ab) + A(bv_k)

So the area below the chord t is:

A( P_t)=A( P )-S_k+S_j-1+A( t' )

so we get:

Theorem 2: Given a simple polygon P with n vertices, there is a data structure that after O(n) preprocessing time can return the area of P below a query chord t in constant time

________________________________________________________________________________

Problem 3 ( Fan Problem): Given 2n rays from the origin construct a data structure which for a query line l crossing all 2n rays can quickly return the sum of the areas of the n triangles A_i bounded by l and the lines 2i-1 and 2i (see Fig.2 )

we are given n lines, with line L_i forming an angle b_i>0 with the x axis, and intersecting it at x=a_i. For a query line Q forming an angle a >0 with the x axis and intersecting it at x=t, let l_i be the signed length of the segment of L_i delimited by Q and the x axis. The sign of l_i will be positive if the intersection with Q is above the x axis, negative otherwise (see Fig 15).

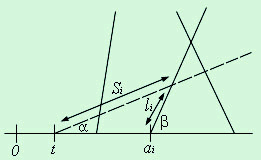
Fig. 15

By using standard trigonometry, we obtain:

For simple discussion, we now apply several restrictions to this problem. for example, suppose n is even, a_i =0, the b_i are in increasing order, t=-1, and for any query, a<b_i for all i (and so t<0). then we get A(Q)

where u=cota, and b_i = cotb_i , note that A(Q) is a rational function in u and that the b_i can take arbitrary values.Then any data structure allowing queries for the fan problem will compute A(Q) accuratly for an infinite number of u's ( i.e. all u> cotb₁ )

Now, construct a polygon P as follows: Starting with our n rays as above, pick three angles a₀< a₁< a₂ <b₁ , and let Q_j be the query line for angle a_j (with t=1). Let p_i,j be the intersection of line L_i with Q_j , i=1, ..., n. P (see Fig. 16)will have the sequence of vertices

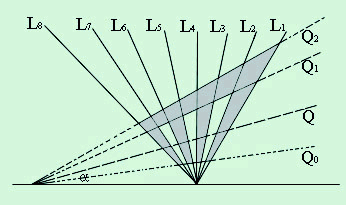
Fig. 16

p_1,0 , p_2,0 , p_2,1 , p_3,1, p_3,0,..., p_2i-1,0, p_2i,0, p_2i,1, p_2i+1,1, p_2i+1,0,..., p_n,0, p_n,2, p_1,2, p_1,0

For any query line Q with angle a, a₀< a< a₁ , the area of upper subpolygon P₁ cutting by Q is

A(P₁)= A(P)- A(Q)+A(Q₀)

Theorem 3 Given a set of rays L={L₁,..., L_n}, and k lines Q₁,..., Q_k each intersecting all n rays, we can compute for each area A(Q) in O((n+k)log²n)

Proof: Because A(Q) is a polynomial, It is known that a polynomial of degree n can be evaluated for k values in O((n+k)log²n) time using FFT (Fast Fourier Transform)

__________________________________________________________________________________