Problem of the 2 Thieves

Two thieves steal an expensive necklace that contains diamonds and rubies on it in no particular order.  Both thieves want to get an equal cut of the diamonds and rubies.  How many times will they have to cut the necklace so that each thief gets half the diamonds and half the rubies?

Answer

1. If the diamonds and rubies are evenly spaced, then we will only have to cut once.  This is the trivial case.

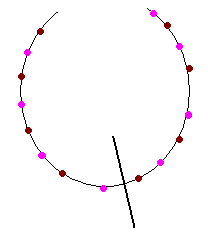
The necklace above only needs 1 cut to equally cut up the necklace!

2. Now suppose that all the diamonds are on one side one side of the necklace and all the rubies are on the other.  To make sure that each thief received an even number of each, we would have to cut the necklace twice.

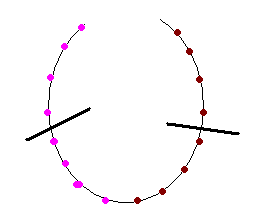The above necklace needs to be cut twice to evenly distribute the diamonds and rubies.

3. Will we ever have to cut it more than twice?
     NO!
     The answer lies in the Ham Sandwich Cut theorem!

Suppose we drape the necklace over a parabola.  We know that any line that cuts a parabola cuts it at most two places.  Therefore, if we find the ham sandwich cut of the necklace, while it is draped over the parabola, the most we will ever have to cut it is twice!

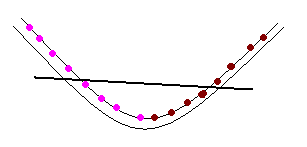Necklace draped over a parabola, with a hamsandwich cut through it!