Axiomatic Origami -- or the Mathematical backbone of paper folding
The most powerful knows set of axioms of Origami was publish by Humiaki Huzita in 1992, in his paper named "Understanding Geometry throught Origami Axioms", published in the Proceedings of the First International Conference on Origami in Education and Therapy (COET91). They provide a framework for mathematical exploration of paperfolding.
Each application of an axiom is akin to folding a sheet, using some features of the sheet, like points and lines, and then unfolding it again.
Axiom 1 -- Folding through 2 points
This is the equivalent of Edge & Compass's edge, directly.
It amounts to drawing a line thru two points.
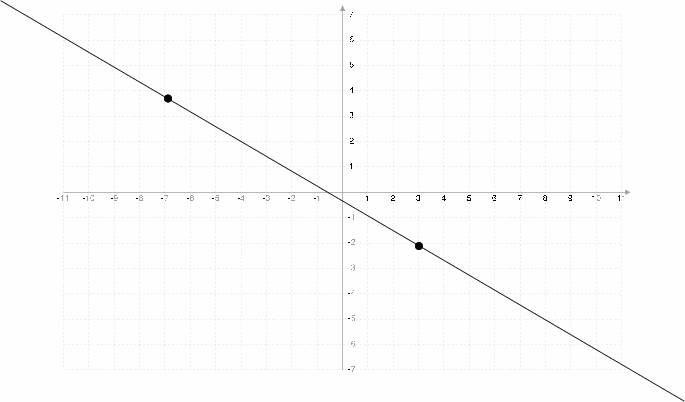
For the more mathematicall oriented, this is the equivalent of solving first degree equations. If you have two points (x0, y0) and (x1, y1) and you are trying to find the equation a*x+b=y of the line, you simply solve for a and b, giving:
- a
- a=(y2-y1)/(x2-c1)
- b
- b=y1-a*x1 or equivalently b=y2-a*x2
Axiom 2 -- Folding a point on another point
This is feasible in Edge & Compass, we're really tracing a perpendicular to the line defined by those two points, intersecting that line exactly in the middle of the segment defined by those two points.
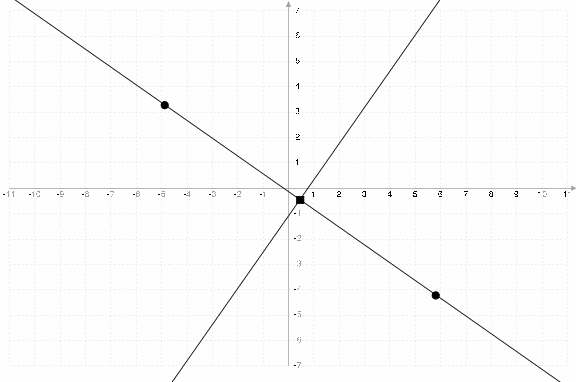
Again, for the math lovers:
- a
- a=-(x2-c1)/(y2-y1)
- b
- b=(y2-y1)/2-a*(x2-x1)
Axiom 3 -- Folding a line on another line
This is also feasible in Edge & Compass.
If the lines are not parallel. It's really just bisecting the angle between those two lines.
If the lines are parallel, one has to build a triangle between the two lines, find the middle of the segments of the triangle and use those midpoints as the basis for the parallel line.
It's worth nothing that the origami way does not care about the relative position of the two lines, the technique does not change.
It's very important to remark that in the case where the lines are not parallel, there are two ways to do this (one for each pair of opposing angles), but only one way if they are parallel.
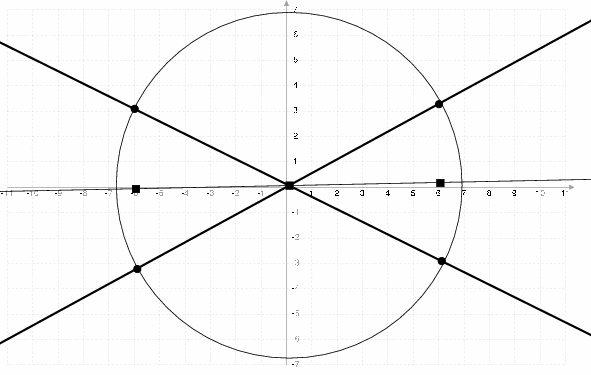
For the mathematically oriented, here's the way to do it with non-parallel lines:
- Find the intersection (x0, y0) of the two lines:
- x0
- x0=(a0-a1)/(b0-b1)
- y0
- y0=(-a1*b0+a0*b1)/(a0-a1)
- Using this point, draw a circle of any radius, and find the two pairs of two points of intersection between a line and the circle:
- Circle
- (x-x0)2+(y-y0)2=0
- Line
- a*x+b=y
- Using those four points (remember you need to do this twice), construct two segments you will then bisect and join the middle of those two segments.
In the great tradition of university folks across the world, I've left the last few steps' equations out. Left as an exercise to the reader.
Axiom 4 -- Folding a line on itself through a point
This is feasible in Edge & Compass, it amounts to finding the perpendicular to a line that goes thru a given point.
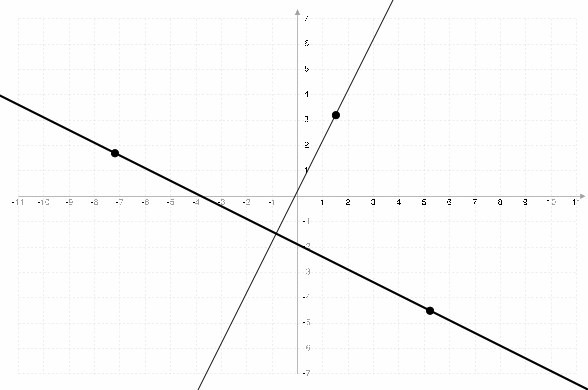
To do this in Edge & Compass, draw a circle thru the point that intersects the line at points A and B. Draw a circle at point A of radius=dist(A, B) and another at B of radius=dist(B, A). Join the two intersections of those last two circles.
And for the followers of Erdos, Euler and Gauss:
- a`
- a`=1/-a
- b`
- b`=y-a`*x
Axiom 5 -- Folding a point on a line through a point
This is the exact same thing as Edge & Compass's compass. You can find the 'intersection' of the circle defined by the articulation point as its center and the distance between the 2 points as its radius.
It's important to remark that it might be impossible to do this, in particular, if the distance between the two points is smaller than the distance between the focus of the fold and the line. If the circle drawn below is tangeant to the line, there's a unique way to do this (the point of tengeance). But if the distance between the line and the focus is smaller than the distance between the two points, there are two points of intersections, thus two possible folds.
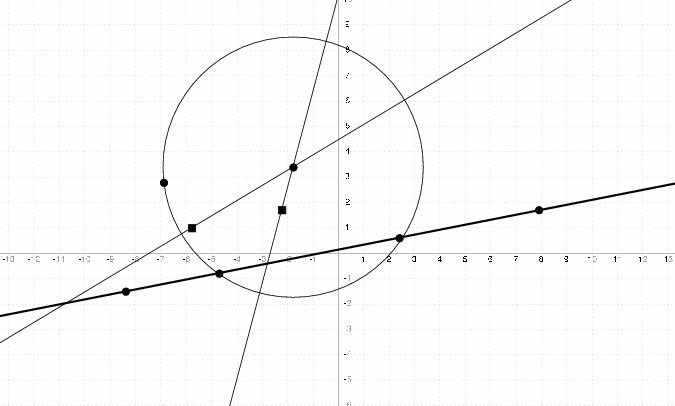
Interestingly, this is isomorphic to solving 2nd degree equations in the RAM Model of Computation. In particular:
- Circle
- (x-x0)2+(y-y0)2=0
- Line
- a*x+b=y
Thus, you are here solving a 2nd degree equation (the circle's). The astute reader will have noted that: Axiom 3 also contains a circle! But this is not a requirement in axiom 3, only the most obvious way to do it (to me, at least). Here, it is a requirement:
- SQRT
- SQRT=(x22+2*x2*b*a+2*x2*y2*a+y22*a2+x12-2*x1*x2+y12-2*y1*y2-b2+2*y2*b+x12*a2-2*x1*x2*a2+y12*a2-2*y1*y2*a2)1/2
- x3
- x3=(2*x2-2*a*b+2*y2*a+2*SQRT)/(2*(1+a2))
- y3
- y3=a*(2*x2-2*a*b+2*y2*a+2*SQRT)/(2*(1+a2))+b
- x4
- x4=(2*x2-2*a*b+2*y2*a-2*SQRT)/(2*(1+a2))
- y4
- y4=a*(2*x2-2*a*b+2*y2*a-2*SQRT)/(2*(1+a2))+b
Axiom 6 -- Folding 2 points on 2 different lines
This Origami's improvement on Edge & Compass. This is impossible in Edge & Compass, and this is isomorphic to solving 3rd degree mathematical equations.
It's important to remark that it might be impossible to do (if the two lines are parallel and the the distance between the two lines is greater than the distance between the two points), or there might be a unique way to do it.
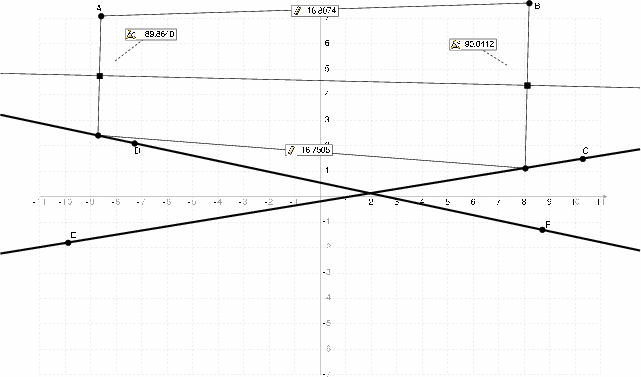
And for the mathematicians amongst us:
- x`1
- x`1=(-a2+x1-b1+b2-y2+y1+x2*a2)/(-a1+a2)
- y`1
- y`1=(-a2*a1*x1+a1*b2+a1*y2+a1*y1+a2*y2*a1-a2*b1)/(-a1+a2)
- x`2
- x`2=(-b1+b2+y1-y2+a1*x1+x2+a1)/(-a1+a2)
- y`2
- y`2=(-a2*b1+a2*y1+a2*y2-a2*a1*x1+a2*x2*a1+a1*b1)/(-a1+a2)