Glossary

Algorithm An algorithm is any procedure for processing input in order to produce output. Everyday examples of algorithms include recipes, wagon assembly instructions, diet plans, and get-rich-quick schemes.

Antipodal Pair of Points An antipodal pair of points consists of two points on the boundary of a polygon such that there exist two parallel lines, one through each point, and every other point in the polygon lies between these two lines. In Figure 4, p₅ and p₉ are an antipodal pair.

Convex Angle A convex angle is less than or equal to 180 degrees.

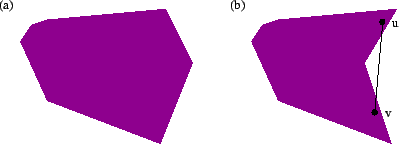
Convex Hull The convex hull of a set of points is the smallest convex polygon containing all points in the set. Informally, if we represent the set of points as nails partially embedded into a wall then the convex hull can be represented as an elastic streched around the nails. See Figure 1(b) for an example. Observe that a set of points has exactly one convex hull.

Convex Polygon A convex polygon can be defined in the following three equivalent ways:

1. A polygon such that if u and v are any two points inside or on the boundary of the polygon then the entire line segment uv lies inside or on the boundary of the polygon.
2. A polygon whose boundary points have convex interior angles.
3. A polygon that is the union of all triangles determined its points.

See Figure 18 for an example of a convex and a nonconvex polygon.

Figure 18: Convex polygon (a) and nonconvex polygon (b).

Diameter The diameter of a set of points is the greatest Euclidean distance between any two points in the set.

Euclidean Distance Euclidean distance is commonly called straight-line distance or distance as the crow flies. Using Cartesian coordinates, the distance between points (x, y) and (x', y') is given by the formula $\sqrt{(x-x')^2 + (y-y')^2}$ in accordance with the Pythagorean theorem.

Interior Angle The interior angle at a point v on the boundary of a polygon is the angle formed by the point and two other points also on the boundary immediately on either side of v. See Figure 19.

Figure 19: Interior angle of a point on a polygon.

Jordan Curve Theorem The Jordan Curve theorem states the following:

Any simple closed curve in the plane partitions the plane into three disjoint connected sets such that the set that is in the curve is the boundary of both the other sets.

This theorem is important for proving properties about polygons because they are simple closed curves.

Local Maximum A point u on the boundary of a polygon is a local maximum for a point v also on the boundary if and only if the boundary points immediately on either side of v are closer to u than v is to u. In the left polygon of Figure 13, v is a local maximum for x.

Monotonic A sequence of values increases monotonically if and only if they never decrease. Conversely, a sequence decreases monotonically if and only if they never increase. For example, the sequence 1, 3, 5, 6, 6, 7, 8 increases monotonically but the sequence 1, 3, 5, 4, 6 neither increases nor decreases monotonically because we have the subsequence 3, 5, 4.

Polygon A polygon is the region of a plane bounded by a finite collection of line segments satisfying the following properties:

1. The edges are connected so that they form a single cyclic chain.
2. Each segment intersects exactly two other segments, one at each endpoint.

Figures 2, 3 and 13 illustrate polygons.

Strictly Convex Angle A strictly convex angle is less than 180 degrees. These differ from convex angles because they cannot equal 180 degrees.

Strictly Convex Point A strictly convex point is a point on the boundary of a polygon whose interior angle is strictly convex. In Figure 2, all strictly convex points on the boundary are labelled.

Unimodality Property A polygon is unimodal iff for every point x on its boundary a traversal of the entire boundary starting at x takes us monotonically further from x and then monotonically closer to x until we arrive back at x. See Figure 13 for examples.