 |
The more interesting case is the Dobkin and Snyder algorithm. Its correctness relies on the following two statements:
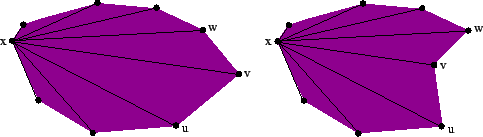
A polygon is unimodal iff for every point x on its boundary a traversal of the entire boundary starting at x takes us monotonically further from x and then monotonically closer to x until we arrive back at x. By monotonically further from x, we mean that our distance from x may remain the same during portions of our traversal but it must never decrease; by monotonically closer, we mean the same except that the distance must never increase. For example, in Figure 13, the left polygon is unimodal with respect to point x because as we traverse the boundary from x to v by way of u, our distance from x continually increases. Then, traversing back to x by way of w our distance from x continually decreases. The right polygon is not unimodal with respect to point x because u and w are further from x than point v between them.
A convex polygon P = (p1, p2, p3, p4) of four points is sufficient to show that not all convex polygons are unimodal. See Figure 14.
The distance between p1 and p2 and between p1 and p4 is 1. The interior angle at p1 is greater than 0 and less than 180 degrees. The length of line segment p1p3 is slightly less than 1 but long enough to intersect p2p4. As a result, p1 has two local maxima: p2 and p4. We can generalize this example to show that, in fact, a point can have n local maxima in a convex polygon described by 2n points. These polygons were originally described in [1]. The distance between every point pi, i even, and p1 is 1. The length of line segment p1pi, i odd, is slightly less than 1 but long enought to intersect line segment pi - 1pi + 1. Thus, all points pi, i even, are local maxima for point p1. The resulting convex polygon for ten points is illustrated in Figure 14.Earlier, we mentioned that the Dobkin and Snyder algorithm actually relies on the assumption that a local maximum is the maximum. In other words, if v is a local maximum of u then v is the furthest point from u. In the polygons just exhibited, this is actually true. However, if we perturb p2n so that the distance between p1 and p2n becomes slightly larger than 1 then the polygon remains convex but local maximum p2 is now closer to p1 than local maximum p2n.