Shamos Algorithm[5]

This third algorithm is quite different from the previous two. We apply the algorithm to the convex polygon P = (p₁, p₂,..., p_n).

Antipodal Pairs

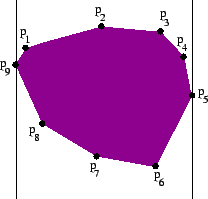
Find all antipodal pairs of points. An antipodal pair of points consists of two points such that there exist two parallel lines, one through each point, and every other point in the polygon lies between these two lines. In Figure 4, p₅ and p₉ are an antipodal pair.

Figure 4: Antipodal Pair

We can picture finding these pairs by rolling the polygon along the ground. The point touching the ground and the point furthest from the ground form such a pair. We record all such pairs. We stop rolling the polygon when the first point to touch the ground returns to the ground.

Diameter

The antipodal pair that is at maximum distance apart achieves the diameter.

For a more formal description of the algorithm see [5,4,9]. The applet below gives an animation of the Shamos algorithm.Can you construct a counterexample?

Click to run the Shamos algorithm.

This algorithm finishes after a constant multiple of n steps because, as we roll the polygon, each of the n points hits the ground exactly once and becomes the furthest from the ground exactly once. Therefore, we have at most 2n steps. Determining the pair at maximum distance from one another is at most another 2n steps. For a more formal proof of optimality see [5].