|
|
|
|
The Two-Ears Theorem
The Two-Ears Theorem was developed and proven by Gary H. Meisters at the University of Nebraska in 1975 [4].
The proof by Meisters is by induction on the number of vertices, n, in the simple polygon P. It is quite elegant.
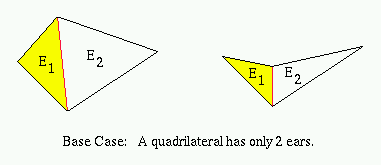
Base Case:
n = 4. The simple polygon P is a quadrilateral, which has two ears.
Induction:
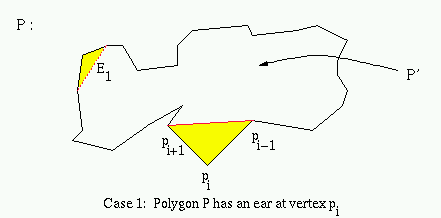
Let P be a simple polygon with at least 4 vertices. Vertex pi is a vertex of P where the interior angle formed by pi-1, pi, and pi+1 is less than 180o.
Case 1:
Polygon P has an ear at pi. If this ear is removed, the remaining polygon P' is a simple polygon with more than three vertices, but with one less vertex than P. By the induction hypothesis, there are two non-overlapping ears E1 and E2 for P'. Since they are non-overlapping, at least one of these two ears, say E1, is not at either of the vertices pi-1 or pi+1. Since all ears of P' are also ears of P, polygon P has two ears: E1 and the ear at pi.
Case 2:
Polygon P does not have an ear at pi. So, the triangle formed by pi-1, pi, and pi+1 contains at least one vertex of P in its interior. Let q be the vertex in the interior of this triangle such that the line L through q and parallel to the line through pi-1 and pi+1 is as close to pi as possible.
Let a and b be the points of intersection of line L with the polygon edges (pi, pi+1) and (pi-1, pi), respectively. The triangle formed by pi, a, and b does not contain in its interior any vertex of P (or else our choice of vertex q would be incorrect).
The line segment Q from vertex q to pi can be constructed without intersecting any edges of P. Line segment Q divides P into two simple polygons: P1 (that contains vertices pi, pi+1,..., q) and P2 (that contains vertices pi, pi-1,..., q).

There are now two sub-cases to consider:
Case 2a:
Polygon P1 is a triangle. So, P1 is an ear for polygon P. By the induction hypothesis, polygon P2 must have at least two non-overlapping ears, E1 and E2 (or else it too would be a triangle and polygon P would have only four vertices). Since they are non-overlapping, at least one, say E1, is at neither vertices pi nor q. E1 does not overlap with the ear formed by polygon P1, so it is the second ear in polygon P.
Case 2b:
Polygon P1 is not a triangle. So, by the induction hypothesis, polygon P1 has two ears, E11 and E12 and polygon P2 has two ears, E21 and E22. Since they are non-overlapping, at least one of the ears in P1, say E11, is not at vertex pi or q. Similarly, at least one of the ears in P2, say E21, is not at vertex pi or q. These two ears, E11 and E21 will be non-overlapping ears for polygon P
Q.E.D.
It is known that a simple polygon can always be triangulated. Leaves in the dual-tree of the triangulated polygon correspond to ears and every tree of two or more nodes must have at least two leaves.
Q.E.D.

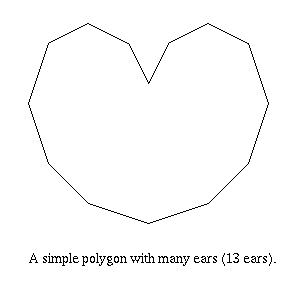
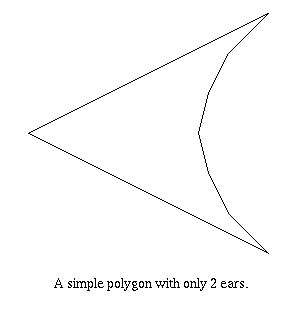
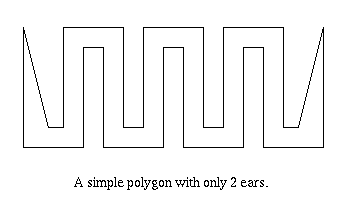
|
|
This page was last updated on Wednesday, December 10th, 1997.
© 1997 Ian Inc.