Introduction to Ear Cutting for Simple Polygons
A polygon is a closed chain of n line segments (pi, pi+1) for 0 <= i <= n-1 and (pn-1, p0) , where n >= 3. The polygon P is represented by its vertices P = (p0, p1,..., pn-1).
2 Polygons
A simple polygon is a polygon P with no two non-consecutive edges intersecting. There is a well-defined bounded interior and an unbounded exterior for a simple polygon, where the interior is surrounded by edges. When referring to P, the convention is to include the interior of P.
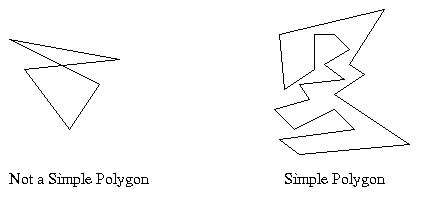
A diagonal is a line segment lying entirely inside polygon P and joining two non-consecutive vertices pi and pj

A vertex pi is called a principal vertex if the diagonal (pi-1, pi+1) intersects the boundary of simple polygon P only at pi-1 and pi+1 [5].
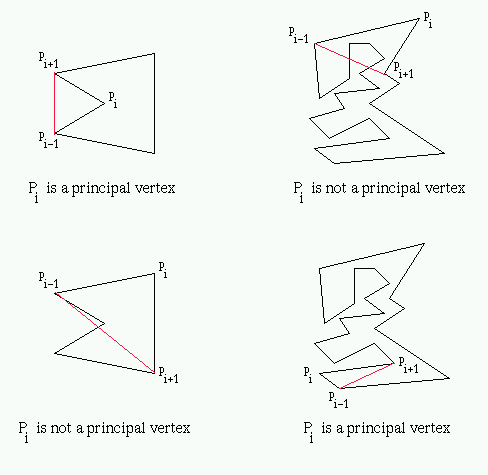
A principal vertex pi of a simple polygon P is called an ear if the diagonal (pi-1, pi+1) that bridges pi lies entirely in P. We say that two ears pi and pj are non-overlapping if the interior of triangle (pi-1, pi, pi+1) does not intersect the interior of triangle (pj-1, pj, pj+1) [4].

This page was last updated on Saturday, December 6th, 1997.
© 1997 Ian Inc.