Glossary
A simple polygon containing precisely two ears and one mouth [7].
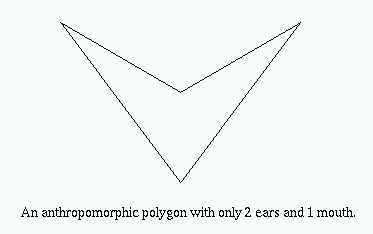
A vertex pi is concave if a left turn is made at pi while going from pi-1 to pi+1 where the interior of the simple polygon P is to the right (ie. P is being traversed in clockwise order).

The convex hull CH(P) of a polygon P is the smallest convex polygon that contains P.
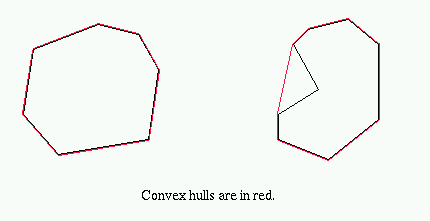
A polygon P is convex if and only if for any pair of points x, y in P the line segment between x and y lies entirely in P.

A vertex pi is convex if a right turn is made at pi while going from pi-1 to pi+1 where the interior of the simple polygon P is to the right (ie. P is being traversed in clockwise order).

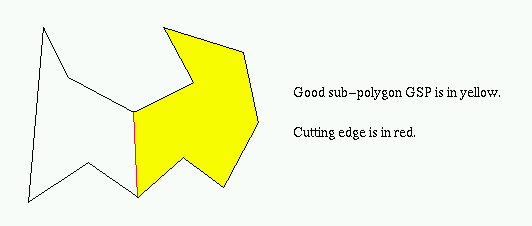
The one edge of a good sub-polygon GSP that is not in simple polygon P (where GSP is a good sub-polygon of P).
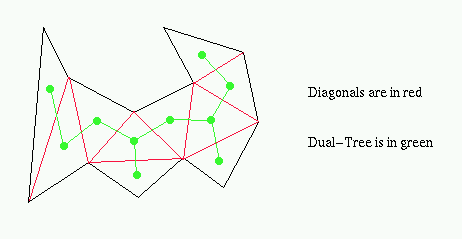
A line segment lying entirely inside polygon P and joining two non-consecutive vertices pi and pj

Given a triangulated simple polygon, the dual-tree is the graph generated by plotting a vertex at each triangle and edges joining vertices in adjacent triangles (triangles which share a diagonal).
A principal vertex pi of a simple polygon P is called an ear if the diagonal (pi-1, pi+1) that bridges pi lies entirely in P. We say that two ears pi and pj are non-overlapping if the interior of triangle (pi-1, pi, pi+1) does not intersect the interior of triangle (pj-1, pj, pj+1) [4].

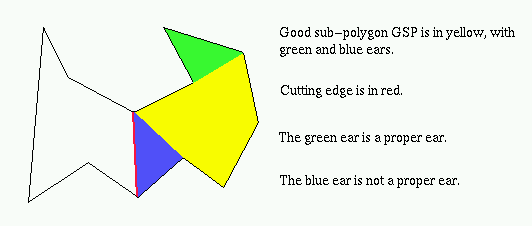
A good sub-polygon of a simple polygon P, denoted by GSP, is a sub-polygon whose boundary differs from that of P by at most one edge. This edge, if it exists, is called the cutting edge [1].

A simple closed curve C in the plane divides the plane into exactly two domains, an inside and an outside [2].
A vertex in a graph with only 1 edge incident to it.

A principal vertex pi of a simple polygon P is called a mouth if the diagonal (pi-1, pi+1) is an external diagonal, i.e., the interior of (pi-1, pi+1) lies in the exterior of P [7].
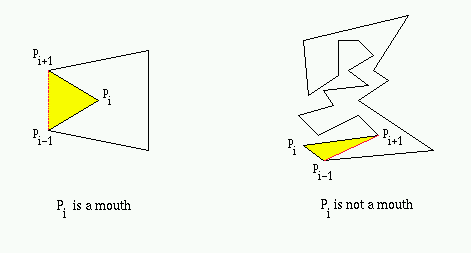
Except for convex polygons, every simple polygon has at least one mouth [7].
A closed chain of n line segments (pi, pi+1) for 0 <= i <= n-1 and (pn-1, p0) , where n >= 3. The polygon P is represented by its vertices P = (p0, p1,..., pn-1).
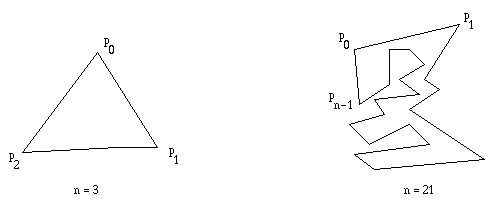
2 Polygons
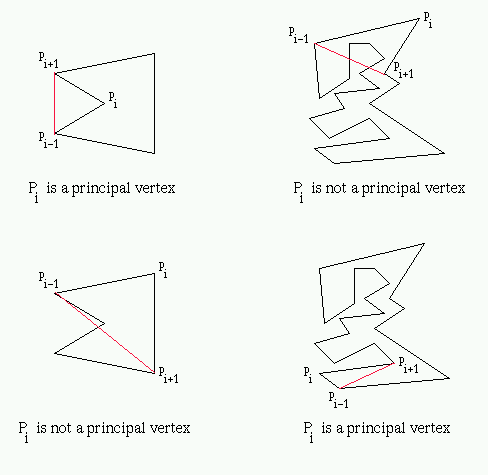
A vertex pi of simple polygon P is called a principal vertex if the diagonal (pi-1, pi+1) intersects the boundary of P only at pi-1 and pi+1 [5].
A proper ear of a good sub-polygon GSP is an ear of GSP which is not an end-point of the cutting edge of P [1].
A polygon P with no two non-consecutive edges intersecting. There is a well-defined bounded interior and unbounded exterior for a simple polygon, where the interior is surrounded by edges. When referring to P, the convention is to include the interior of P.
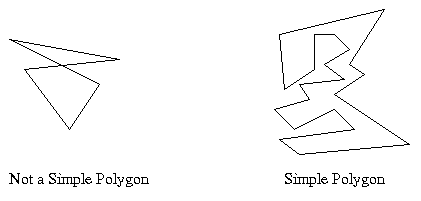
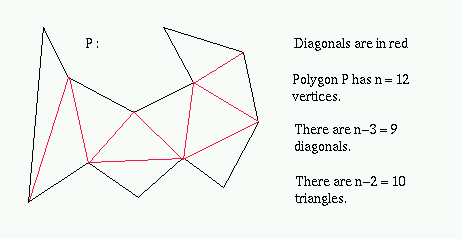
A triangulation of a simple polygon consists of n-3 non-intersecting diagonals or n-2 triangles where n is the number of vertices in the simple polygon.
Except for triangles every simple polygon has at least two non-overlapping ears [4].
This page was last updated on Wednesday, December 10th, 1997.
© 1997 Ian Inc.