| Shape Discovery :: A Simple Algorithm :: |
Let's proceed with a description of the algorithm.
Initialization
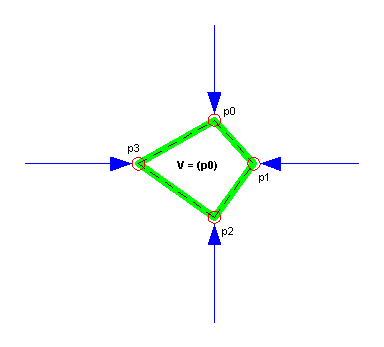
The first step consists of probing the shape on two orthogonal lines from all four directions. Remember that the shape contains the origin. We are thus guaranteed to hit four distinct points by aiming towards the origin. The initial current hull H has four vertices. The shape is not empty and contains the origin so none of the vertex triplets are colinear. As a result all edges are initially unverified and V contains only the starting point p0. The following figure illustrates the result of the initialization phase. See the previous section for the legend.

Iteration
Remember that V contains a sequence of m points such that all edges including [pm-1, pm] are verified. Once the setup is completed, the algorithm repeatedly tries to extend the set V by verifying the next unverified edge [pm, pm+1]. The first iteration, for example, tries to verify the unverified edge [p0,p1]. An unverified edge is probed using the method described in the intuition section. Let's explain the method again, this time using the appropriate vocabulary that we defined in the previous section.
Consider the situation in the following diagram. The edge [a,b] is the last verified edge in the sequence V. We wish to verify the next edge, namely edge [b,c]. The edges [a,b] and [c,d] are first extended in the direction of the edge [b,c] until they meet at some point x. The probe is sent in the direction from point x to a point on the edge [b,c] such that the probe bisects the angle bxc. This choice of angle is not critical but is reasonable since the probe should be aimed to reduce uncertainty as much as possible.
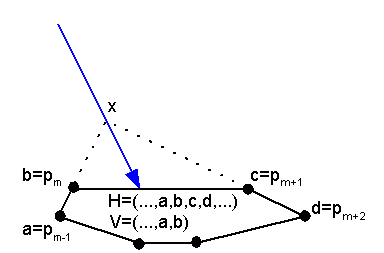
As explained in the intuition section, one of three outcomes results.
Outcome 1
|
|
Outcome 2
|
|
Outcome 3
|
|
As explained in intuition, the orientation of the edges [a,b] and [c,d] may be such that they never join at a point x. In such a case the probe is sent in the direction of the edge [b,c] resulting either in the second or third outcomes as shown above.
Notice that at each iteration, either the current hull is extended (outcome 3) or the set V is extended (outcomes 1 and 2). In other words, we either add an unverified edges or verify an edge.
Termination
The iterations are repeated until there is no unverified edge. At that point, the set V has been extended so that it forms a closed polygon (p0 = pm).
|
|
Terminology and Data Structures |
Analysis |
|