Shape Discovery :: A Simple Algorithm ::

Analysis

In this section we analyze the algorithm to prove both its correctness and an upper bound on the number of probes. Two observations are made about the data structures. It is shown that these two observations or inductive hypothesis hold all through the execution of the algorithm. These observations are then used to prove the correctness and complexity of the algorithm. 

Observation 1

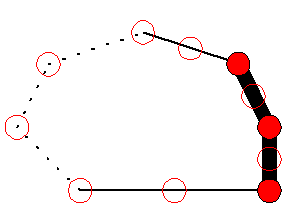
The set of verified edges of H forms a contiguous sequence. [1]

This fact follows from our definition of the algorithm. Initially none of the edges are verified. The algorithm picks a starting point and tries to verify the first edge. It then keeps trying to verify the next unverified edge. Whenever the algorithm attempts to verify an edge, we are guaranteed that the edge that immediately precedes it has already been verified. Thus the verified edges of H form a contiguous sequence. The following diagram shows an example of a sequence of verified edges. See the vocabulary section for the appropriate legend. (dotted lines: unverified; thin line: semi-verified; thick line: fully-verified)



Observation 2

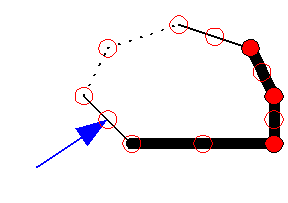
At most one edge in H doesn't have these properties:

1. Semi-verified edges have exactly one contact point in their interior.
2. Fully-verified edges have either 1 or 2 contact points in their interior.

The exceptional edge, if there is one, has 3 internal contact points if fully-verified and 2 internal contact points otherwise. The exceptional edge is the first edge in V and the last one to be fully-verified.

By observation 1, we know that the verified edges form a contiguous sequence. Until the end, the first and last edges in the sequence are semi-verified. All the verified edges between these two semi-verified edges are fully-verified. Indeed a verified edge surrounded by two verified edges is bounded by two verified vertices and thus fully-verified. This fact is illustrated in the diagram above.

Let's consider a semi-verified edge at the end of the sequence of verified edges in H. Assume that it only has a single internal contact point. Consider, for example, the semi-verified edge at the bottom of the above diagram. The next probe can result in three outcomes as explained in the previous section. We will review the three cases here.
Outcome 1

The last semi-verified edge of the sequence is extended to include an extra point for a total of two internal contact points. This edge is now a fully-verified edge with two internal contact points and can no longer be extended.

Outcome 2

The final vertex of the last semi-verified edge becomes verified and the edge itself becomes fully-verified with only one internal contact point.
Outcome 3

The semi-verified edge remains semi-verified and still has only a single contact point.

These three cases represent all possible probe outcomes. As a result semi-verified edges have a single internal contact point and fully-verified edges have either one or two internal contact points. The only exception is due to the final edge that gets fully verified. Under some special circumstances, the first edge of the sequence will have two internal contact points while semi-verified and three contact points when fully-verified. This situation occurs when the first two contact points in the initial sequence of four fall on an edge of the polygon but not on the vertices. This is illustrated in the following animation.


Conclusions

These observations allow us to reach some conclusions about the correctness and complexity of this algorithm. First notice that there can be no more than n verified edges since there are n edges in the polygon. In the end we thus have a total of n fully-verified edges corresponding to the true edges of the polygon. Observation 2 tells us that each fully-verified edge has a maximum number of two internal contact points, except one edge which might have three internal contact points. The maximal number of probes is thus 3n+1 (2n+1 internal contact points plus n vertices). 

The simple algorithm requires at most 3n+1 probes to discover the shape of an n-vertex polygon.

The algorithm keeps verifying unverified edges in sequence, always verifying the edge following the last verified edge. At each step, either the number of verified edges is increased or the number of unverified edges increases. The algorithm stops only when all edges are verified, which implies that the correct polygon is found. Moreover we have already seen that the number of probes is bounded so the algorithm will stop. The algorithm is thus correct.

Algorithm

An Improved Algorithm