Intuition

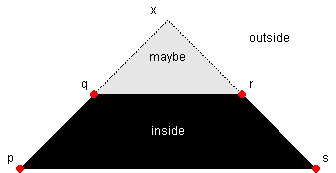
This shape discovery algorithm is based on a simple intuition. Consider the situation shown in the diagram below. The points p, q, r and s are contacts points obtained by probing. The gray triangle is a typical region of uncertainty resulting from such a convex hull (see here). It is obtained by extending the edges neighboring the [q,r] edge of the convex hull.

Where should we probe next? Intuitively it makes sense to send our probe in the direction of the qrx triangle to maximize our chances of reducing the shape uncertainty. In order to improve our next probe, we can investigate two hypothesis:

Hypothesis 1

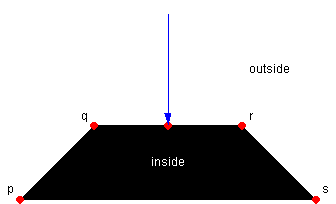
The line [q,r] is an edge of the polygon. If this hypothesis is true, a probe sent towards any point within the line [q,r] results in a contact points on that line. 

Hypothesis 2

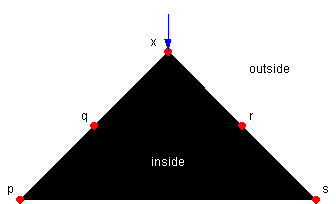
The lines [p,x] and [s,x] are both edges of the polygon. This hypothesis can be verified by sending a probe in the direction of the point x. 

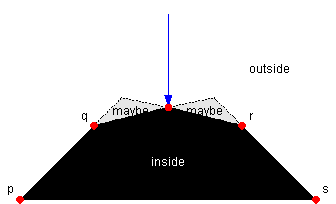
Notice that these two hypothesis can be verifying simultaneously by sending a probe that goes through both the point x and one of the points of the [q,r] line. This probe can have three outcomes as described below.

Outcome 1  The probe hits the point x confirming the first hypothesis.
Outcome 2 The probe hits a point on the [q,r] line confirming the second hypothesis.
Outcome 3 The probe hits the polygon at some other point within the qrx triangle. Both hypothesis are refuted but progress has been made.

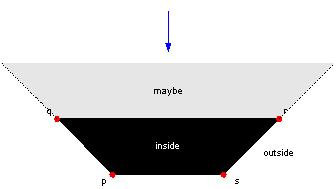
This method can be applied whenever the surrounding convex hull edges ([p,q] and [r,s] in this example) can be elongated to form a triangle. In other situations, the maybe region does not form a triangle and may even be infinite. The best we can do then is assume that the convex hull edge under consideration is a true edge of the polygon and send a probe in its direction. This is illustrated in the following diagram.

A Simple Algorithm

Terminology and Data Structures