| Isomorphic Triangulation of Simple Polygons | Diana Garroway | |
|
||
Isomorphism
Informally, an isomorphism is a map that preserves sets and
relations among elements. [MathWorld]
Spiderweb Connectivity
The spiderweb connectivity is simply a method for connecting a set
of vertices. These vertices each have a
weight assigned to them and this weight is interpreted as the distance
from the vertex to a centre point in the end connectivity. For
example, if we have 9 vertices and they have the weights of <3, 1,
4, 3, 3, 4, 2, 4, 3>, then we will insert extra (Steiner) points such
that the minimum path from each of the vertices
to a centre point is given by the weight. This
is best illustrated by the following figure. If
we think of the connectivity in layers, then each at each layer, the
Steiner points connect to there neighbouring vertex of that layer. If there is not a neighbouring vertex of that
layer (for example if the neighbour has smaller weight), then the point
will simply be connected to its neighbour. We
also connect the path from the vertex to the centre, through the
Stiener points. In the end we get a
connection on the vertices that looks similar to a spiderweb. The
spiderweb connectivity can be created for any set of vertices and
weights and yields triangles and quadrilaterals. The
quadrilaterals can simply be triangulated.
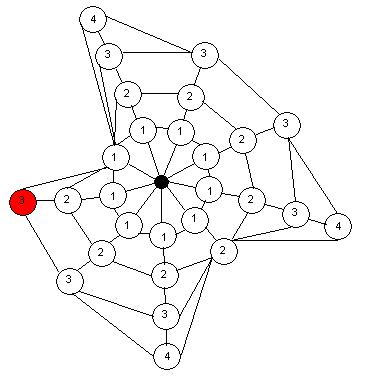
Figure 1: The spiderweb connectivity for the sequence
<3, 1, 4, 3, 3, 4, 2, 4, 3>, starting at the red vertex.
Steiner Point
An extra point added to a vertex set that was not part of the
original set. (Also called Steiner Vertex).