| Isomorphic Triangulation of Simple Polygons | Diana Garroway | |
|
||
Isomorphically
triangulating two simple polygons.
The algorithm outlined here was
presented in [4]. It will produce
isomorphic triangulations of any two simple polygons. We will
show the algorithm using the following two polygons as an example.
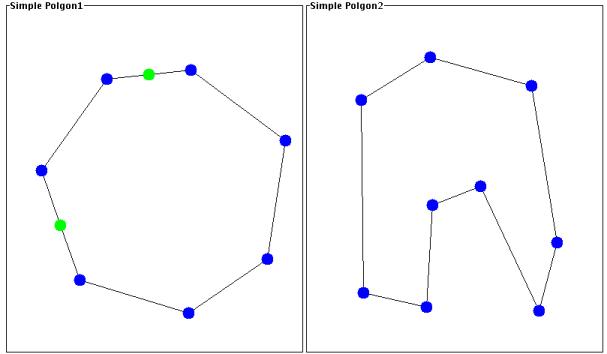
Step 1:
Adjust the cardinality of the polygons.
If the two polygons do not
have the same number of vertices, then add vertices to the smaller
polygon, along its edges, until they both have the same number.
The green vertices have been added in the following figure.
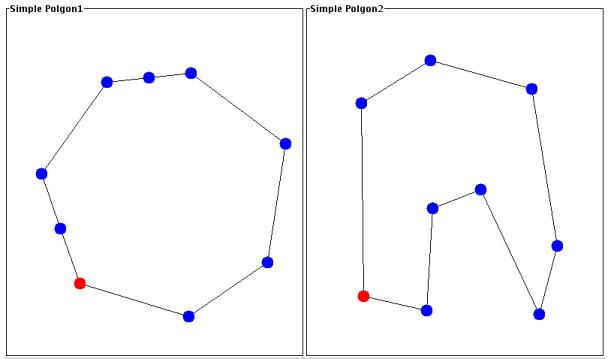
Step 2: Pick two corresponding vertices.
Before creating the
triangulations, we decide upon the correspondence between the vertices
of the 2 polygons. By picking 1 vertex from each to be a
corresponding pair, we then map the rest of the vertices in a clockwise
order from these two. In the figure below, the red vertices were
chosen to be the corresponding pair.
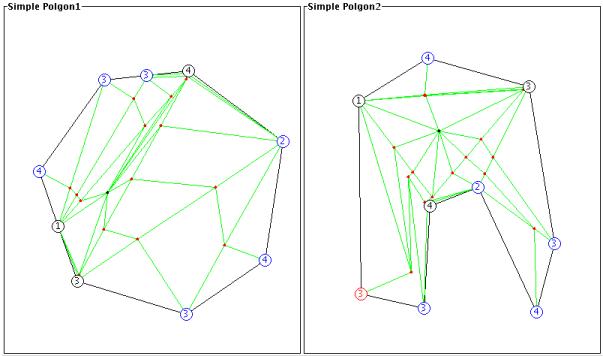
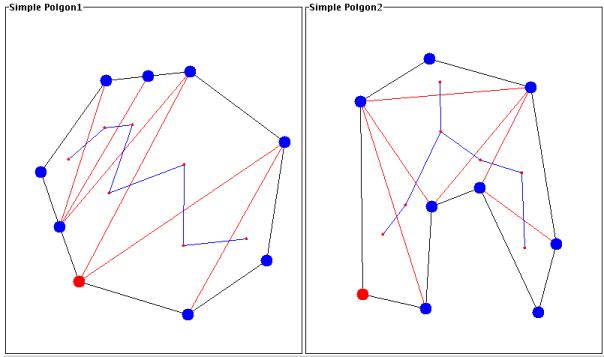
Step 3: Triangulate and Find
the dual tree
The next step is to triangulate each polygon, using any
triangulation algorithm, and then to find the dual tree of each
polygon. This step is shown in the following figure.
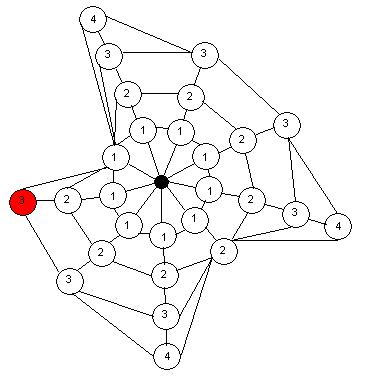
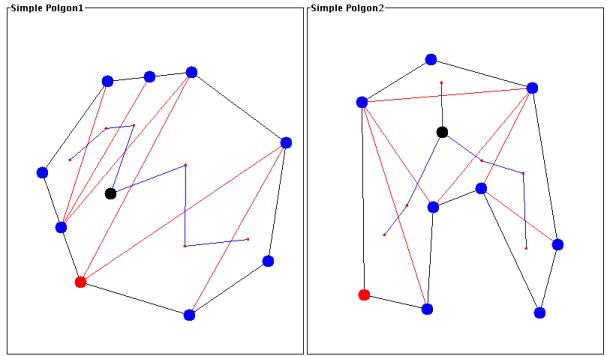
Step 4: Find the centre
vertex of the dual trees.
For each of the dual trees, find the centre vertex of the
tree. In the figure below, the centre vertex is shown as the large
black dot.
Step 5: Assign weights to
each of the polygon vertices.
For each of the vertices, assign it a weight based on the
following method:
1. For each
vertex in the dual tree of the polygon, calculate the length of the
path from it to the center vertex.
2. Each of
these vertices is at the centre of a triangle of the original
triangulation. Assign each triangle the path length +1 as its
weight.
3. Each of
the vertices of the original polyon is a vertex of at least 1
triangle. For each vertex, look at the triangle(s) that it is a
part of and find
the triangle with the
minimum weight. Assign the vertex to have this weight.
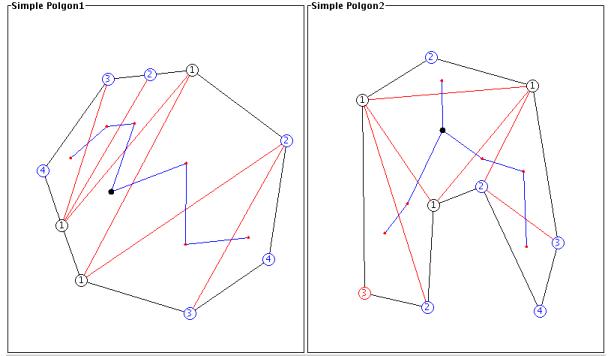
This concept is shown in the following figure. Notice that each
polygon vertex is a part of one or more triangles and the each vertex
of the dual tree is at the centre of one triangle. The weight
given to each polygon vertex is the minimum path length of the dual
tree vertices of the associated triangles, to the centre vertex
(+1). The weights are shown at each vertex in the following
figure and the 3 vertices which form the center triangle are
highlighted in black.
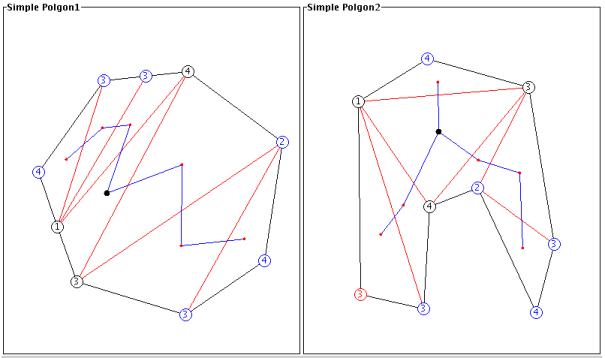
Step 6: Adjust the vertex
weights to be the maximum of the corresponding pairs.
For each of corresponding vertex pairs, assign the one with
lower weight the weight of the other vertex. In the polygon on
the left, since the vertex we chose as the corresponding vertex is also
a center vertex, it is colored black instead of red, but it is still
our corresponding vertex.
Step 7: Find the spiderweb
connectivity for the vertex weights and embed it into each polygon.
For each polygon, take the vertex weights as the sequence
for the spiderweb connectivity and embed the spiderweb into the
polygons. The figure below shows the spiderweb connectivity for
the vertex weights and the following figure shows the connectivity
embedded into the polygons. Notice that for each vertex of the
polygon, the mimimum path from that vertex to the center vertex the
vertex weight.