Introduction
Complexity
The Art-Gallery
The Proofs
Conclusions
References
NP-Completeness and Reduction
Reduction
Definition 1: For any two languages, say A & B, we say A is reducible to B, denoted A < B, if and only if there exists an f such that:
- For all x in A, f(x) is computable in deterministic polynomial time
- For all x, x is in A if and only if f(x) is in B
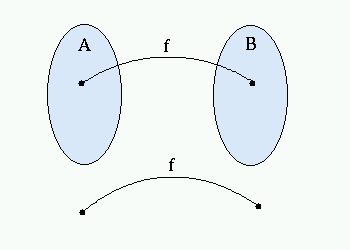
If there is a deterministic polytime function that maps 'yes'-instances in A to 'yes'-instances in B and 'no'-instances in A to 'no'-instances in B then A is reducible to B. Alternatively, this is called 'Karp-reduction' so we can say 'A is Karp-reducible to B'. More intuitively, if A < B, we can say A is 'no harder' than B. Here is a graph of said mapping f:
NP-Completeness
Definition 2: A language L is NP-complete if and only if:
- L is in NP
- For any language L' in NP, L' < L
So a language is NP-complete if it is in NP, this is obvious. Also, every other language in NP must be no harder than it. Thus, we are homing in on the 'hardest' problems in NP.
Theorems and Proof Styles
Theorem 1: Given languages A & B, both in NP, with A being NP-complete and A < B, then B is NP-complete.
Proof: Consider an arbitrary language L in NP. Since A is NP-complete, then L < A. This implies that there is some function f, computable in deterministic polytime that maps according to definition 1. Since A < B, then there is some g, computatble in deterministic polytime that maps according to definition 1. If we combine those functions according to function composition, we get fog that is both computable in polytime and maps according to definition 1. Thus all languages in NP reduce to B. Finally, since B is in NP then B is NP-complete.
This is the standard manner to prove that something is NP-complete. First, find an existing NP-complete problem and reduce it to the one you want to prove NP-complete. Most NP-completeness proofs are of this kind with the exception of Cook's original proof and a few others. Cook proved that deciding whether or not a boolean formula had a satisfying assignment was NP-complete in 1971. It was the first NP-complete problem and from there hundreds of problems have been proved NP-complete.