Introduction
Complexity
The Art-Gallery
The Proofs
Conclusions
References
NP-Hardness for Polygons without Holes
Now we deal with the problem of art galleries whose floor plans have no holes. This may seem like an easier problem since it's just a k-holed polygon where k is 0 but that restriction fails in our earlier proof since the polygon had to have at least 1 hole per variable.
So the problem definition is the same but the reduction will be different. We will refer to the new problem without holes to be StarC.
First, for each occurence of a literal, we construct a spike as in figure 7. The point p is visible only from either point t or point f. No other vertex will be able to see p. So one of t or f will have to be chosen in order to guard the point p. The choice of t or f will correspond to the choice of true or false, respectively.
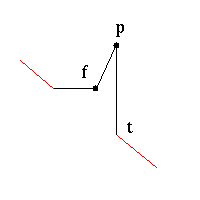
Fig 7: "Spike" literal pattern
Next, we add three of those literal spikes to create a clause junction. A sample junction is shown in figure 8. We know that for each i = 1, 2, 3, one of {ti, fi} must be assigned a guard. Also, in order to cover the shaded triangle, one of {t1, t2, t3} must have a guard on it. In other words, at least one of the literals must be true in order for the clause junction to be covered and thus, for the clause to be satisfied.
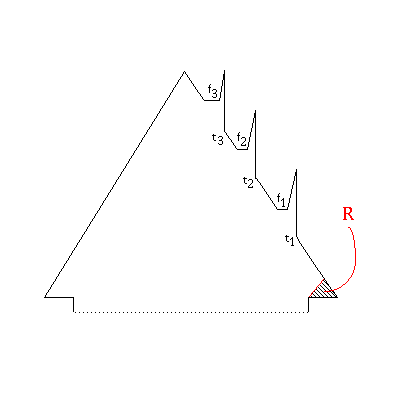
Fig 8: A clause junction/polygon
Now, one may have noticed that it would be possible, at this stage, for the same literal to have both true and false value in different literal spikes. We can force all literal spikes representing the same literal to have the same value by creating variable wells. This pattern is illustrated in figure 9. It consists of two wells, with a vertex at the top of the left well called F, and a vertex at the corresponding position of the right well called T. Also, each well will have s thin spikes , where s is the number of clauses in which the variable u participates. These spikes will be aligned with the F or T vertex depending on the well in which it is found. Also, for the point q to be seen, one of {T, F} will have to have a guard on it. No other guards will be required to see the rest of the well if the literals for this assignment have consistent truth values.
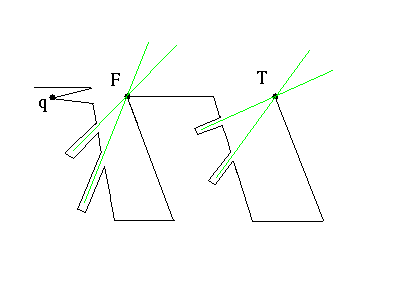
Fig 9: The wells which maintain consistent variable assignment
To guard the wells, one guard alone would not regularly suffice. A quick look will suffice to prove this. Luckily, by our construction, it is possible to guard the wells if there is a consistent way of assigning values to the variables and making the original boolean value true. This is how. Let u be some variable with T and F on it's pair of wells. Each spike in a well is aligned with either T or F and also, with a literal (in a clause junction far away) of either u or !u. Thus a spike in the left well will be collinear with F (always) and the t or f of the literal if it's true or false (respectively). The case is symmetric for a spike in the right well.
So, if for every literal, we assign all ui's the same value of true/false, then all spikes in the right/left well of ui's variable wells will be covered. Now we need only cover the T or F node of the wells, whichever will cover the other set of spikes.
Finally, notice that we can see down all the wells with a guard on point x. So, we will cheat and allow one there. So we will need 3 guards for each clause, 1 variable for each variable well and 1 guard for x. Thus the total number of guards for which we wish to test minimality will be K = 3m + n + 1.
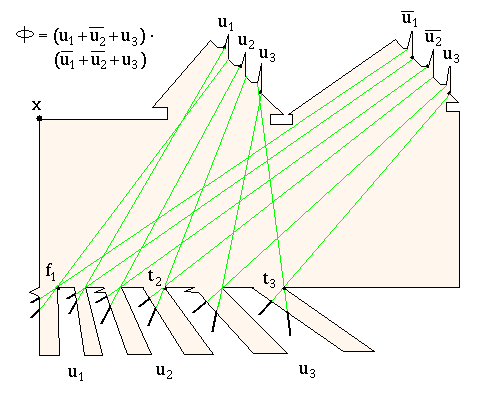
Fig 10: A sample polygon for the formula
Finally, we need only to prove that our construction meet the requirements. As we process each literal and each clause only once, we clearly have a polynomial time algorithm. Suppose there is way to satisfy the original 3SAT boolean formula with some assignment set. Choose the t's and f's in the clause junctions accordingly, this will necessarily cover the clause junctions by construction. Then set the corresponding T or F in the variable wells for each literal. Finally, put one guard on x. This will take precisely K guards but will always cover the polygon.
Now, assume there exists a guard cover of less than K guards. One guard must be on x, otherwise K would not be enough. The remaining guards need to cover the points outlined in the construction. Then, we examine the variable wells and choose T or F depending on which one is covered. That choice of T/F must lead to a satisfying and consistent variable assignment to the formula.