Proof of Theorem 1.1

Theorem 1.1 states the following: Let x and y be two points in a set of points S. If x and y achieve the diameter of S then x and y are strictly convex points.

We begin the proof with the following lemma showing that any point at the ``corner'' of a convex hull (i.e. strictly convex point) belongs to the set of points determining the convex hull.

Lemma A.1   Every strictly convex point on the convex hull determined by a set of points S belongs to S.

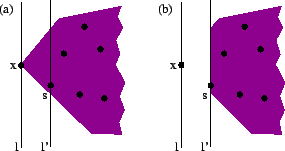
PROOF By way of contradiction, assume that some strictly convex point x on the hull does not belong to S. Because the interior angle at x is strictly convex it is possible to construct a line l through x that intersects the convex hull only at x. Let y be one of the points in S closest to l and construct another line l' through y parallel to l. This situation is illustrated in Figure 15(a). Point x is the only point shown that is not in S.

Figure 15: Illustration for proof of Lemma A.1

Because the convex hull is a convex polygon and y is the closest point in S to l, all other points in S either lie on l' or on the side of l' opposite x. Therefore, we can construct a new smaller convex polygon, as in Figure 15(b), containing all points in S by removing x and all other points in the convex hull on the same side of l' as x.

This is a contradiction because the convex hull is defined to be the smallest convex polygon containing all points in S. Therefore, all strictly convex points on the convex hull determined by a set of points S belong to S.$\Box$

Let x and y be two points in a set of points S that achieve the diameter of S. By way of contradiction, assume that y is not strictly convex. Point y either lies inside or on the boundary of the hull.

If y lies on the boundary of the hull but is not strictly convex then, because the hull is a convex polygon, y lies on a line segment zz' where z and z' are strictly convex points on the hull. By Lemma A.1, z and z' belong to S. At least one of them is farther from x than y. This is a contradiction because x and y achieve the diameter of S.

If y lies inside the hull then by the Jordan Curve Theorem we can extend the line segment xy past y until it intersects the boundary of the hull. Because the hull is a convex polygon, this intersection point lies on the line segment zz' where z and z' are strictly convex points on the hull. By Lemma A.1, z and z' belong to S. At least one of them is farther from x than y. Once again, this is a contradiction because x and y achieve the diameter of S.

Therefore, x and y must be strictly convex points on the convex hull determined by S.

Back to Theorem 1.1...