Proof :
Let's name P the perpendicular to ab at a. The fact
that P is a supporting line of A comes from the definition of Hausdorff
distance. As illustrated below, if a is the furthest point of A
relative to b, then a circle C centered at b and of radius
ab will completely enclose A. Because C contains all points of A,
then its tangent to a is a supporting line of A.
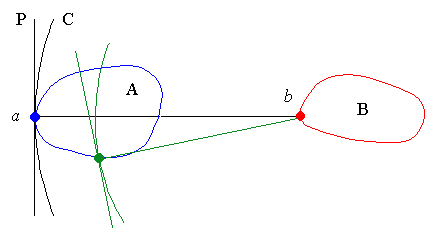
The second part of lemma 1a says that A and B are on the same side of P. This is can be proved by contradiction : if some points of A are not on the same side of P than B, then the point of support (shown in green above) is not the furthest point of A from b. This point of support thus can not define the Hausdorff distance h(A, B).