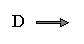Glossary
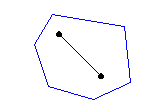
| Convex polygon : |
A polygon is said convex if the line that joins any two points of
the polygon is entirely inside the polygon.
|
||||||||
| Metric : |
A function D, usually called distance, that respects the following
properties when applied to x, y and z :
|
||||||||
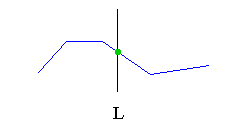
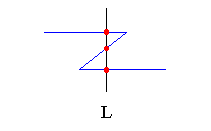
| Monotone chain : |
A chain C (i.e. a sequence of edges) is said to be monotone in a direction D if any line L orthogonal to D intersects C in exactly one point.
A polygon P is monotone in some direction if an orthogonal line intersects
P in no more than two points ; a convex polygon is monotone
in any direction.
|
||||||||
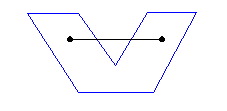
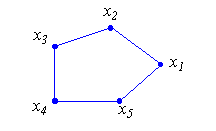
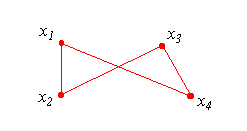
| Simple polygon : |
A polygon with no self-intersecting edges. Since a polygon is defined by a sequence
of vertices, a priori nothing prevents any self-intersection of its edges.
|
||||||||
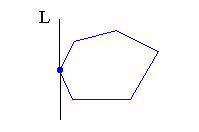
| Supporting line : |
Straight line L passing through a vertex of a polygon P, such that the
interior of P lies entirely on one side of L. The supporting line is a
generalization of the tangent.
|