Computing all lex-positive bases
representing a given vertex
For details about lrs options visit: http://cgm.cs.mcgill.ca/~avis/C/lrslib/USERGUIDE.html
Let us start with a cross polytope in 4 dimensions.
sony% cat cross4.ine
cross
H-representation
begin
16 5 rational
1 -1 1 1 1
1 -1 -1 1 1
1 -1 1 -1 1
1 -1 -1 -1
1
1 -1 1 1 -1
1 -1 -1 1
-1
1 -1 1 -1
-1
1 -1 -1 -1
-1
1 1 1 1 1
1 1 -1 1 1
1 1 1 -1 1
1 1 -1 -1 1
1 1 1 1 -1
1 1 -1 1 -1
1 1 1 -1 -1
1 1 -1 -1
-1
end
If you run lrs on this file you see that it is degenerate with each of
its 8 vertices having 6 lex-pos bases.
1. We select vertex 0 1 0 0 and ask for all lex-pos bases
that contain it.
It is contained on 8 facets in the file cross4.ine: all of the facets
with a +1 in column 3.
Add the normals of these facets together to get an objective function
z= 8 x2 that maximizes at 0 1 0 0.
2. Now run lrs in linear programming mode to get a lex-pos basis for
the vertex 0 1 0 0.
To do this add the following 3 lines to the end of cross4.ine
maximize 0 0 8 0 0
lponly
printcobasis 1
Running lrs we get:
sony% lrs cross4.ine
*lrs:lrslib v.4.2c,
2010.7.7(32bit,lrsmp.h)
*Copyright (C) 1995,2010, David
Avis avis@cs.mcgill.ca
*Input taken from file cross4.ine
cross
*maximize: 0
0 8 0 0
*printcobasis 1
V#1 R#0 B#1 h=0 facets 8 10
12 14 I#8 det= 8 in_det= 8
1 0 1
0 0
*LP solution only requested
3. We now use the cobasis 8 10 12 14 to do an lrs run on
cross4.ine with the truncate option.
Replace the three options for the lp only run with:
startingcobasis 8 10 12 14
allbases
printcobasis 1
truncate
Run lrs and you get the following output:
sony% lrs cross4.ine
*truncate
V-representation
begin
***** 5 rational
V#1 R#0 B#1 h=0 facets 8 10
12 14 I#8 det= 8 in_det= 8
1 0 1
0 0
V#2 R#0 B#2 h=1 facets 8 12
14 16 I#8 det= 8 in_det= 8
1 0 1
0 0
V#3 R#0 B#3 h=2 facets 8 12
15 16 I#8 det= 8 in_det= 8
1 0 0
1 0
V#4 R#0 B#4 h=2 facets 12 14
15 16 I#8 det= 8 in_det= 8
1 -1 0 0 0
V#5 R#0 B#5 h=2 facets 8 14
15 16 I#8 det= 8 in_det= 8
1 0 0
0 1
V#6 R#0 B#6 h=1 facets 4 8
10 12 I#8 det= 8 in_det= 8
1 0 1
0 0
V#7 R#0 B#7 h=1 facets 10 12
14 15 I#8 det= 8 in_det= 8
1 -1 0 0 0
V#8 R#0 B#8 h=1 facets 6 8
10 14 I#8 det= 8 in_det= 8
1 0 1
0 0
V#9 R#0 B#9 h=2 facets 4 6 8
10 I#8 det= 8 in_det= 8
1 0 1
0 0
V#10 R#0 B#10 h=3 facets 2 4
6 10 I#8 det= 8 in_det= 8
1 0 1
0 0
end
*Tree truncated at each new vertex
*Totals: vertices=10 rays=0
bases=10 integer_vertices=4
4. You obtain a list of the 6 lex-pos cobases that represent 0 1 0 0
and
also 4 other cobases that you simply discard.
The reverse search tree corresponding to step 3 is below.
To see how it is constructed, note it is a depth first search tree
based on the height parameter h=integer in the above output.
Note that their are 6 vertices adjacent to 0 1 0 0 on the polytope of
which 3 are computed, and one, (-1,0,0,0) appears twice.
So this is not equivalent to computing the vertex figure at 0 1 0 0.
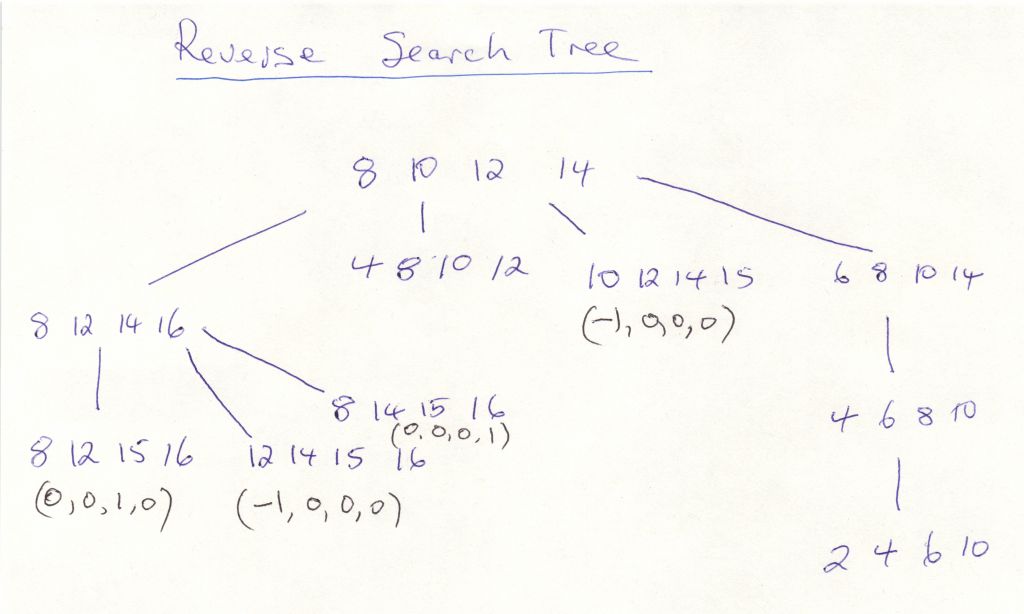
To understand this tree, it is useful to compute all lex-pos bases of
the polytope by running step 3 with 'truncate' removed.
In the full reverse search tree containing 48 notes, we see that the
cobases 4 8 10 12 and 2 4 6 10 are leaves of the tree, so no
truncation is performed.
The remaining 38 nodes of the tree are all in subtrees of the truncated
vertices. The maximum depth is 8.
(If anyone cares to draw this tree and send it to me, I am happy to
post it :-) )
