What's new
Introduction
lrs:
installation and usage
mplrs: installation and usage
lrsnash: installation and usage
File formats
Basic options
Arithmetic packages
Estimation
Extreme point
enumeration and eliminating redundant inequalities
Linear programming
Fourier elimination
(New)Testing redundancy in
projections
Volume and triangulation
Voronoi Diagrams and Delaunay
Triangulations
Linearities
Timing, interrupts and restarts
(New)Vertex/Facet
cross reference listing
Error messages and
troubleshooting
Hints and comments
Acknowledgements and References
Introduction
A polyhedron can be described by a list of inequalities (H-representation)
or as by a list of its vertices and extreme rays (V-representation).lrs
is a C program that converts a H-representation of a polyhedron
to its V-representation, and vice versa. These problems are
known respectively at the vertex enumeration(VE) and convex
hull(CH) problems.
Fukuda's FAQ page
contains a more detailed introduction to the problem, along
with many useful tips for the new user.
lrs is based on the reverse
search algorithm developed with Komei Fukuda, see (AF1992)
, modified to use lexicographic pivoting and implemented in
rational arithmetic. It uses limited multithreading via OpenMP. (Av1998a)
contains a technical description, and (Av1998b)
contains some computational experience.
mplrs is a full parallel
version of lrs based on Open
MPI for distributed systems, developed with Skip Jordan, see (AJ2015).
The input files are in Polyhedra format , developed with
Fukuda. The format is essentially self-dual, and the output file
produced can be read in as an input file, with very minor
modifications, to perform the reverse transformation. This format
is compatible with that used in Fukuda's
cddlib package, which performs the same
transformations using a version of the double description
method. The program normaliz
provides a parallel version of the double description method.
Another program using the same file format is the primal-dual
method pd,
developed by Bremner, Fukuda and Marzetta . It is
essentially dual to lrs, and
is very efficient for computing H-representations of simple
polyhedra, and V-representations of simplicial polyhedra. It will
compute the volume of a polytope given by an H-representation.
Links to additional VE/CH programs are given here.
Polyhedra handled by lrs need not be full
dimensional and may contain input linearities and redundant
columns . lrs accepts either integer or rational
input, and produces integer or rational output. All computations
are done exactly using hybrid arithmetic, starting with 64 bits
and moving to 128 bits and extended precision (GMP or built-in) if
necessary, see (AJ2021).
Since it is a pivot based method, lrs can be very slow for
degenerate inputs: i.e. H-representations of non-simple polyhedra,
and V-representations of non-simplicial polyhedra. On the other
hand, it does not store the vertices/ rays or facets produced, so
for very large problems it may be the only method that can solve
the problem. Using mplrs, even with just a few cores,
significantly speeds up the computation. A discussion of various
vertex enumeration/convex hull methods and the types of polyhedra
that cause them to behave badly is contained in (ABS
1997). A more recent discussion with extensive empiral
tests can be found in (AJ2017).
Considerable technical assistance over several decades has been
provided by David Bremner.
Functions of mplrs/lrs
include:
Redundancy removal involves the removal of any inequalities that are
not required to represent the polyhedron in an H-representation. For
a V-representation it is the problem of evaluating the extreme
points and extreme rays. Finding a minimum representation involves
locating any hidden linearities in the input file. These problems
are normally considerably easier than the H to V and V to H
transforamtions performed as they are performed by linear
programming. In some cases, redundancy can greatly slow the
processing time taken for H-V transformation using
lrs/mplrs, and it is advisable to remove any redundancy
and hidden linearities from the input file before starting a long
run.
These programs can be distributed freely under the GNU GENERAL
PUBLIC LICENSE. Please read the file COPYING carefully before
using. Please inform the authors of any interesting
applications for which these programs were helpful.
lrslib
installation and usage
Package install is the simplest for linux or WSL/linux users, but
may not contain the latest version of lrslib:
Debian/Ubuntu (2025.3.25: v7.1):
sudo apt install lrslib (maintained by
David Bremner <bremner at debian.org> )
Fedora (2025.3.25: v7.3):
sudo dnf install lrslib (maintained by
Jerry James <loganjerry at gmail.com> )
Additional instructions for installing
mplrs, a multithreaded
implementation of lrs using
MPI, are here.
Precompiled binaries lrs,
lrsgmp for some Linux, Apple and Windows
machines are here.
These may be slower for problems requiring very long
integers.
Install from source code:
- From lrs home page, click on "Download" and retrieve the file
lrslib-073.tar.gz
- Unpack with:
% gunzip lrslib-073.tar.gz
% tar xvf lrslib-073.tar
- Go to the new directory
% cd lrslib-073
- make lrs with various arithmetic packages (it may be
necessary to edit makefile to set the path to the gmp library)
% make
(compilers with __int128 support)
This produces binaries lrs
(hybrid arithmetic) and the usually slower lrsgmp
(GMP arithmetic)
For compilers without __int128 and/or OpenMP support you will need to edit the makefile as indicated at the beginning of that file.
- You will need to have write permission to /tmp to run the
hybrid arithmetic programs lrs.
Temporary files are normally removed before termination.
- If you do not have GNU MP installed you can try using
the built in lrs arithmetic
package:
% make allmp
alternatively you can edit the makefile to compile with
mini-gmp.c , a subset of GMP. (new v7.3)
- Test the program
We will convert the H-representation of a cube given cube by 6 the
six inequalities -1 <= xi <= 1 , i=1,2,3 in the
input file:
% cat cube.ine
cube.ine
H-representation
begin
6 4 rational
1 1 0 0
1 0 1 0
1 0 0 1
1 -1 0 0
1 0 0 -1
1 0 -1 0
end
to the
output file:
% lrs cube.ine
*lrs:lrslib v.7.3 2024.1.31(64bit,lrslong.h,overflow checking)
*Input taken from file cube.ine
cube.ine
V-representation
begin
***** 4 rational
1 1 1 1
1 -1 1 1
1 1 -1 1
1 -1 -1 1
1 1 1 -1
1 -1 1 -1
1 1 -1 -1
1 -1 -1 -1
end
*Totals: vertices=8 rays=0 bases=8 integer_vertices=8
This is a list of the 8 vertices with each co-ordinate +/- 1.
The ***** should be replaced by the actual number, 8, of vertices.
Since lrs does not save the output produced, it does not
know this value until the execution terminates. This output is now
essentially the same as file cube.ext. To complete the test type:
Now the output produced is essentially the
file cube.ine, with the inequalities appearing in a different
order.
- Binaries produced by % make lrs or %
make lrsgmp
lrs
hybrid arithmetic
package starting with 64 bit arithmetic, then
128 bit, then GMP.
lrsgmp
GMP arithmetic only
Additional instructions for installing mplrs,
a multithreaded implementation of lrs
using MPI, are here.
File formats
Example files can be found in the directories ine and ext which
come in the standard distribution. File formats were developed
jointly with Komei Fukuda and are compatible with
cdd . The cdd manual contains additional information and
examples.
The input for lrs is a H- or V- representation of a
polytope. These files have the following formats:
H-representation
name
H-representation
{options}
{linearities
}
begin
m n rational
{list of inequalities }
end
{options}
name is a user supplied name for the
polytope. If the line H-representation is omitted,
H-representation is assumed. The input coefficients are
read in free format, and are not checked for type. Coefficients
are separated by white space. Normally this file would be saved
with filename suffix .ine but this not required.
Comments may appear before the begin or after the end, and to
avoid interpretation as an option, should begin with a special
character such as "*" or "#".
The integer m is the number of inequalities, and the
integer n is the dimension of the input +1.
A list of inequalities contains the coefficients of inequalities
of the form
a0 + a1 x1 + ... + an-1
xn-1 >= 0.
This inequality is input as the line
a0 a1 ... an-1
The coefficients can be entered as integers or rationals in the
format x/y.
For example, the square centred at the origin with side length
two has inequalities
1 + x1 >= 0 1+ x2
>=0 1-x
1 >=
0
1-x2 >=0
and would be represented by the input file
square
*centred square of side 2
H-representation
begin
4 3 rational
1 1 0
1 0 1
1 -1 0
1 0 -1
end
V-representation
name
V-representation
{options}
{linearities
}
begin
m n rational
{list of vertices and extreme rays}
end
{options)
name is a user supplied name for the
polytope. The line V-representation is required. The
input coefficients are read in free format, and are not checked
for type. Coefficients are separated by white space. Comments may
appear before the begin or after the end, and to avoid
interpretation as an option, should begin with a special character
such as "*" or "#".Normally this file would be stored with
filename suffix . ext, but this is not required.
The integer m is the number of vertices and rays,
and the integer n is the dimension of the input +1.
Each vertex is given in the form
1 v0 v 1 ...
vn-1
Each ray is given in the form
0 r0 r 1 ...
rn-1
where r0 r 1 ...
r n-1is a point on the ray.
There must be at least one vertex in each file. For bounded
polyhedra there will be no rays entered.
The coefficients can be entered as integers or rationals in the
format x/y.
For example, the unit square centred at the origin has vertices
(1,1) ,(1,-1),(-1,1),(-1,-1)
and would be represented by the input file
square
*centred square of side 2
V-representation
begin
4 3 rational
1 1 1
1 1 -1
1 -1 1
1 -1 -1
end
The positive quadrant has vertex (0,0) and rays (1,0) (0,1) and
is represented
quadrant
*positive quadrant
V-representation
begin
3 3 rational
1 0 0
0 1 0
0 0 1
end
Its H-representation contains the inequalities x1 >=
0
and
x2 >= 0 :
quadrant
*positive quadrant
H-representation
begin
2 3 rational
0 1 0
0 0 1
end
Note for cdd users: lrs
uses essentially the same file format as cdd. Files prepared
for cdd should work with little or no modification. Note
that the V-representation corresponds to the "hull" option in
cdd. Options specific to cdd can be left in the input
files and will be ignored by lrs. Note the input files
for lrs are read in free format, after the line m n rational lrs will look for
exactly m*n rationals or integers separated by white space
(blank, carriage return, tab etc.). lrs will not
"drop" extra columns of input if n is less than the number of
columns supplied.
lrs has many options to allow various functions to be
performed, and to modify the output produced. Almost all options
are placed after the end statement, maintaining
compatibility with cdd. Where this is not the case, it
will be mentioned explicitly. All options are optional.
allbases
This option instructs lrs to list each vertex (or facet)
for each of its bases. Normally a vertex (or facet) is only output
when its lex-min basis is found, to avoid duplications - see
section Output Duplication
. This option is often
combined with printcobasis .
bound x
// Use with H-representation - for lrs or nash //
Either the maximize or minimize
option should be selected. x is an integer or rational.
For maximization (resp. minimization) the reverse search tree is
truncated whenever the current objective value is less
(resp. more) than x .
cache n
lrs stores the latest n dictionaries in the reverse
search tree. This speeds up the backtracking step, but requires
more memory. If n is set to one, there is no caching and
"pure" reverse search is performed. The default is n=50 . At the end of a run a message gives cache
information. The output
*Dictionary Cache: max size= 4 misses=
10/1340 Tree Depth=5
indicates that with cache size set to 4, only 10 of the
1340 dictionaries computed were not in the cache during
backtracking and had to be recomputed. The maximum tree depth
was 5, so there would be no misses with a cache size of 6. Full
caching reduces processing time by about 40%.
debug
startingbasis endingbasis
Print out cryptic but detailed trace, dictionaries
etc. starting at #B=startingbasis and ending at #B=endingbasis.
debug 0 0 gives a complete trace.
digits n
//
placed
before the begin statement//
n is the maximum number of decimal digits to be used. If this is
exceeded the program terminates with a message (it can
usually be restarted). The default is set to about
100 digits. At the end of a run a message is given informing the
user of the maximum integer size encountered. This may be used
to optimize memory usage and speed on subsequent runs (if doing
estimation for example). The output:
*Max digits= 45/100
indicates that the maximum integer encountered had 45 decimal
digits, and the program allowed up to 100 digit integers.
dualperturb
If lrs is executed with the maximize or minimize option, the reverse search
tree is rooted at an optimum vertex for this function.
If there are mulitiple optimum vertices, the output will often
not be complete. This option gives a small perturbation to the
objective to avoid this.
A warning message is given if the starting dictionary is dual
degenerate.
eliminate
k i1 i2 ... ik
new in v7.2
(H-representation) Eliminates
k variables in an H-representation corresponding to cols i1 i2 i ... ik
by projection onto the
remaining variables using the Fourier-Motzkin
method. Variables are eliminated in the order given
and redundancy is removed
after each iteration.
(V-representation)
Delete the k given columns from the input matrix and remove
redundancies (cf. extract where redundancies
are not removed).
Column indices are between 1 and n-1 and column zero
cannot be eliminated. The output is a valid lrs input
file.
See Fourier
elimination, also project
and extract
estimates k
Estimate the output size. Used in conjunction with maxdepth - see
Estimation.
extract k i1
i2 ... ik (lrs only) v7.2
(H-representation)
A preprocessing step to remove linearities (if any) in an
H-representation and resize the A matrix. The
output as a valid lrs
input file. The resulting file will not contain any equations
but may not be full dimensional as there
may be additional
linearities in the remaining inequalities. Options in the
input file are stripped. The user can specify
the k columns i1 i2 ... ik
to retain otherwise if k=0 the columns are considered in the
order 1,2,..n-1. Linear dependent
columns are skipped and
additional indices are taken from 1,2,...,n-1 as
necessary. If there are no linearities in the input
file the given columns
are retained and the other ones are deleted.
(V-representation)
Extract the given columns from the input file outputing a
valid lrs input file. Options are stripped.
(See also eliminate
and project)
geometric
//
H-representation
or voronoi option only //
With this option, each ray is printed immediately after each
vertex with which it is incident.
Parallel rays will get output many times.
For more information and an example see Geometric Rays in Hints and Comments .
incidence
This
option automatically switches on printcobasis , so see below for
a description of this option first.
Can be used with printcobasis n. (Ver
4.2b)
For input H-representation, indices of
all input inequalities that contain the vertex/ray that is
about to be output. For a simplicial face, there is no new
output, since these indices are already listed. Otherwise,
the additional tight inequalities are listed after a colon.
Eg:
V#1 R#0 B#1 h=0 facets 12 14 15
16 : 9 10 11 13 I#8 det= 8
1 0 0 0 1
The vertex 0
0 0 1 satisfies 8 input inequalities
as equations, as indicated by I#8 : those with indices 12,14,15,16 are in the cobasis, and those with indices
9, 10, 11, 13 are in the basis. For a ray:
V#1 R#5 B#1 h=0 facets 5 9* 10
11 12 13 : 2 3 4 I#8 det= 8
0 1 1 0 0 1 1
Here the ray 1 1
0 0 1 1 lies on 8 inequalities, with indices 5 10 11 12 13 in basis and
2 3 4 in cobasis. The starred index 9* indicates that the ray is terminated by the
input inequality 9. This inequality is in the cobasis and
defines the vertex from which the ray starts.
For input V-representation, indices of
all input vertices/rays that lie on the facet that is about
to be output:
F#5 B#3 h=2 vertices/rays 7 8*
11 13 15 : 1 3 5 9 I#8 det= 16
1 -1 0 0 0
The facet generated by inequality x1
<= 1 contains 8 input vertices, as indicated by I#8:
those with indices 7,11,13,15 are in the cobasis, and those with indices 1 3 5 9 are in the basis.The starred index 8* indicates that this vertex is also in
the cobasis, but is not contained in the facet. It arises
due to the lifting operation used with input
V-representations.
#incidence
The same as printcobasis.
Included for compatability with cdd.
linearity k i1 i2
i ... ik
The input contains k linearities in rows i1 i2 i ... ik
of the input file are equations. See Linearities.
maxdepth k
The search will be truncated at depth k.
All bases with depth less than or equal to k will be
computed. k is a non-negative integer, and this
option is used for estimates - see
Estimation.
Note: For H-representations, rays
at depth k will not be reported. For V-representations, facets
at depth k will not be reported.
maximize a0 a1 ... an-1
// H-representation only //
minimize a0 a1 ... an-1
//
H-representation
only //
If used with
lrs the starting vertex
maximizes (or minimizes) the function a
0 + a
1
x
1 + ... + a
n-1 x
n-1.
The dualperturb option may be needed to avoid dual degeneracy.
See Nash Equilibria and
Linear
Programming
After
n cobases have been generated lrs terminates and returns
restart data for all unexplored roots of subtrees (except
for leaves which are output). These subtrees are the
unexplored siblings on the path back to the root of the
reverse search tree. Used by mplrs to
break up large subtrees into smaller pieces.
maxincidence n
k //from v.7.3//
Prunes the search tree when the depth is at least k and the
current vertex/facet has incidence at least n.
Using verbose a message is printed
whenever the search tree is pruned.
maxoutput n
Limits number of
output lines produced (either vertices+rays or facets) to n
mindepth k
Backtracking
will
be terminated at depth k, for k a non-negative integer. This
can be used for running reverse search on subtrees as separate
processes, e.g. in a distributed computing environment.
nonnegative
// This option must come before the begin
statement//
//H-representation
only
//
Bug:
Can only be used if the origin is a vertex of the polyhedron
For problems where the input is
an H-representation of the form b+Ax>=0, x>=0 (ie. all
variables non-negative, all constraints inequalities) it is
not necessary to give the non-negative constraints explicitly
if the nonnegative option is used. This option cannot be used
for V-representations, or with the linearity option
(in which case the linearities will be treated as
inequalities). This option may be used with redund , but the
implied nonnegativity constraints are not tested themselves
for redundancy. To test everything it is necessary to enter
the nonnegativity constraints explicitly in the input file.
(In Ver 4.1, the origin must be a vertex).
printcobasis
k
Every k'th cobasis is printed. If k is
omitted, the cobasis is printed for each vertex/ray/facet that
is output. For a long run it is useful to print the
cobasis occasionally so that the program can be restarted if
necessary.
H-representation: If
the input is an H-representation the cobasis is a list the
indices of the inequalities from the input file that define the
current vertex or ray. For example, with input cube.ine a
typical output is:
V#5 R#0 B#5 h=1 facets 3 4 5 I#3
det=1
1 1 1 -1
This indicates that the vertex (1,1,-1) is
defined by the 3rd, 4th and 5th facet inequalities in the
input file being satisfied as equations. It is the (B#)5th
basis computed, and there have been (V#)5
vertices and (R#)0 rays output up to this point. I#3 means
that this vertex is incident with 3 input inequalities, ie. it
is non-degenerate. See option incidence
above for more information.
For rays, a cobasis is also printed. In
this case the cobasis is the cobasis of the vertex from which
the ray emanates. One of the indices is starred, this
indicates the inequality to be dropped from the cobasis to
define the ray. For example the output:
V#1 R#6 B#4 h=1 facets 2 4* 5 7
I#3 det=1
0 1 1 2 1
indicates that the ray (1,1,2,1) emanates
from a vertex with cobasis defined by input inequalities 2 4 5
7 satisfied as equations. The ray is defined by dropping the
equation with index 4. Note that there may not appear any
vertex in the output with cobasis 2 4 5 7, since the
corresponding vertex may be degenerate and printed with
another (the lex-min) cobasis. To find out which vertices
correspond to which rays, use also the geometric
option. Now the output may appear:
V#1 R#6 B#4 h=1 facets 2 4* 5 7
I#3 det=1
0 1 1 2 1 * 1 0 0 0 0
This indicates that the ray is incident to
the origin. Alternatively, if the allbases option
is used, all cobases will be printed out.
V-representation: If the input is a V-representation, the
cobasis is a list of the input vertices /rays that define the
current facet. For example, with input file cube.ext a typical
output is:
F#5 B#4 h=3 vertices/rays 2 3 4
5* I#3 det= 8
1 0 0 -1
There have been 5 facets output up to this
point, and 4 bases have been computed. This facet is defined
by the vertices in positions 2,3,4 in the input file. The
additional cobasis index 5* appears because a V-representation
is lifted to one higher dimension before processing, and this
index fills out the cobasis. I#3 means that this facet is
incident with 3 input vertices/rays, ie. it is non-degenerate.
See option incidence above for more information.
To initiate lrs from this facet
all 4 indices must be given in this order (omit the *), eg.
startingcobasis 2 3 4 5
Similarly, all 4 indices must be given in
order to restart from this facet:
restart 5 4 3 2 3 4 5
printslack
// Use with H-representation //
lrs
prints a list of the indices of the input inequalities that are
satisfied strictly for the current vertex, ie. corresponding
slack variable is positive.
If nonnegative is
set, the list will also include indices n+i for each decision
variable xi which is positive.
project k
i1 i2 ... ik
new in v7.2
(H-representation) Project the
polyhedron onto the
k
variables corresponding to cols
i1 i2 ... ik
using the Fourier-Motzkin
method. Column
indices are between 1 and n-1 and column zero is automatically
retained. Variables not contained in the list
are eliminated using a
heuristic which chooses the column which minimizes the product
of the number of positive and negative
entries. Redundancy
is removed after each iteration using linear programming.
(V-representation)
Extract the k given columns from the input matrix and remove
redundancies. Column indices are between 1
and n-1 and column zero is
automatically extracted (cf. extract where redundancies are not
removed).
The output as a valid lrs
input file. See
Fourier
elimination, also
eliminate
and
extract
redund start
end
new in v7.1
Check input line numbers
from start to end and remove any redundant
lines.
redund 0 0 will
check all input lines. See redund
redund_list k i1 i2 ... ik
new
in v7.1
Check the k input line numbers with
indices i1
i2 ... ik from
and remove any redundant lines. See
redund
restart V# R# B# depth {facet #s or
vertex/ray #s}
[integervertices n]
/* new in V 7.0 */
lrs can be restarted from any known
cobasis. The calculation will proceed to normal termination.
All of the information is contained in the output from a printcobasis option. The order of the indices is
very important, enter them exactly as they appear in the
output from the previously aborted run.
For H-representation inputs, if the number of integer vertices
is known then the integervertices n
option may also be included. This will ensure that the final
integer vertex count is correct.
To restart from the following cobasis when 2 integer vertices
have already been found:
V#5 R#0 B#5 h=1 facets 3 4 5
det=1
enter:
restart 5 0 5 1 3 4 5
integervertices 2
For a V-representation input:
F#5 B#4 h=3 vertices/rays 2 3
4 5* det= 8
1 0 0 -1
enter
restart 5 4 3 2 3 4 5
Note that if some cobasic index is
followed by a "*", then the index only, without the
"*", is included in the restart line.
Caution:
When restarting, output
from the restart dictionary may be duplicated, and the final
totals of number of vertices/rays/facets may reflect this.
startingcobasis i1 i2 i
... in-1
This allows
the user to specify a known cobasis for beginning the reverse
search. i1 i2
i ... in-1 is a list of the inequalities (for
H-representation) or vertices/rays (for V-representation) that
define a cobasis. If it is invalid, or this option is not
specified, lrs will find its own starting cobasis. For
example, with cube.ine, the user can start at vertex (-1,1,-1)
by specifying:
startingcobasis 1 3 4
startingcobasis
1 3 4
testlin
(before the begin line only)
H-representation only (new 7.3)
redund: An LP test will be made for
hidden linearities at the beginning of the run and is
reported. If there are no hidden linearities one LP per
constraint tests for redund:ancy. If hidden linearities
exist two LPs per constraint search for hidden linearities and
remove redundancies. In both cases the run ends with a
minimum set of linearities and inequalities (ie. no hidden
inequalities or duplicates) and the dimension is reported.
lrs. If neither redund or
redund_list options are present the initial LP test is made,
reported and the run halted. Otherwise same as redund
above.
mplrs: this option
is ignored. In redund/minrep mode a minimum representation
is always found.
threads n
(new in 7.3) lrs only
Multithreading now used by lrs for the V/H-representation transformation using OpenMP for a parallel for loop at depth
0 in the search tree. Disabled for mplrs. If n is not
specified the default OpenMP max threads is used.
truncate // H-representation only
//
The reverse search tree is
truncated(pruned) whenever a new vertex is encountered.
Note:
This does note necessarily produce the set of all vertices
adjacent to the optimum vertex in the polyhedron, but just a
subset of them. See here
for a description of how to use this option.
verbose
Print slightly more detailed
information about the run.
volume
// V-representation only //
voronoi
// V-representation only - place
immediately after end statement //
Arithmetic
packages (Major
update in v.7.1)
lrs/mplrs use hybrid arithmetic with overflow checking,
starting in 64bit fixed integers, moving to 128bit (if available)
and then GMP.
Typically inputs that can be solved in 64bits run 3-4 times
faster than with GMP and inputs solvable in 128bits run twice as
fast as GMP;
Single arithmetic versions are available for comparing
arithmetic packages.
A number of arithmetic packages are supported by lrslib. A
typical installation uses:
lrslong
Fixed length long integer arithmetic. 64-bit and 128-bit(when
the compiler supports it) with overflow
checking
lrsgmp An
interface to GNU MP which must be installed first from https://gmplib.org/.
If your C compiler does not support 128-bit integers you will need to
edit the makefile.
Overflow checking is conservative to improve performance:
eg. with 64 bit arithmetic, a*b
triggers overflow if either a or b is at least 2^31, and a+b triggers an overflow if either a or b is
at least 2^62.
% make single
produces the binaries :
lrs1/lrsnash1
fixed 64 bit, stop on
overflow
lrs2/lrsnash2
fixed 128 bit, stop on overflow
lrsgmp/lrsnashgmp
gmp extended precison arithmetic
and if the FLINT package has been installed ( available at http://www.flintlib.org/
)
lrsflint
FLINT multiple precison arithmetic
lrs1/lrs2 produce a
restart file that can be used instead of redoing the whole
run from the beginning
If you remove the flag -DSAFE in the
makefile then (mp)lrs1 and (mp)lrs2 will not do overflow
checking and will run about 10% faster.
However, if overflow occurs the results are unpredictable:
caveat emptor!
% make singlemplrs
produces the binaries :
mplrs1
64 bit integers with overflow checking. Terminates when
overflow condition is detected.
mplrs2 128 bit integers with overflow
checking. Terminates when overflow condition is detected.
mplrsgmp(default mplrs) use only gmp extended
precison arithmetic (same as lrs in lrslib-062)
lrslib also has support for the
multi-precision FLINT package that needs to be installed from http://www.flintlib.org/
% make flint
produces the
binary lrsflint
% make mplrsflint
produces the binary mplrsflint
Comparisons
(mp)lrs1 runs 3-5 times faster than
(mp)lrs on highly combinatorial polytopes.
(mp)lrsflint performed similarly to (mp)lrsgmp even on
combinatorial polytopes.
Experimental results will be reported at a later date.
Examples
% lrs mp5.ine mp5.ext
*lrs:lrslib v.6.3 2018.4.11(64bit,lrsmp.h)
*Input taken from file mp5.ine
*Output sent to file mp5.ext
*Totals: vertices=32 rays=0 bases=9041 integer_vertices=16
*Dictionary Cache: max size= 17 misses= 0/9040
Tree Depth= 16
In this case 64 bit arithmetic was
sufficient to compute all vertices.
% lrs mit.ine mit.ext
*lrs:lrslib v.7.0 2018.5.1(64bit,lrslong.h,overflow checking)
*Input taken from file mit.ine
*Output sent to file mit.ext
*overflow possible: restarting with longer precision arithmetic
from /tmp/lrs_mit.ine_restart
*lrs:lrslib v.7.0 2018.5.1(128bit,lrslong.h,overflow checking)
*Input taken from file /tmp/lrs_mit.ine_restart
*Output sent to file mit.ext
*Totals: vertices=4862 rays=0 bases=1375608 integer_vertices=477
*Dictionary Cache: max size= 50 misses= 1053/1374992
Tree Depth= 101
*367.370u 1.819s 9616Kb 0 flts 0 swaps 0 blks-in 712 blks-out
In this case 64-bit arithmetic triggered an overflow condition so 128-bit lrs2
was used with a restart.
% lrs c30-15.ext c30-15.ine
*lrs:lrslib v.7.0 2018.5.1(64bit,lrslong.h,overflow checking)
*Input taken from file c30-15.ext
*Output sent to file c30-15.ine
*overflow possible: restarting with longer precision arithmetic
from /tmp/lrs_c30-15.ext_restart
*lrs:lrslib v.7.0 2018.5.1(128bit,lrslong.h,overflow checking)
*Input taken from file /tmp/lrs_c30-15.ext_restart
*Output sent to file c30-15.ine
*overflow possible: restarting with longer precision arithmetic
from /tmp/lrs_c30-15.ext_restart
*lrs:lrslib v.7.0 2018.5.1(64bit,lrsgmp.h) gmp v.6.1
*Input taken from file /tmp/lrs_c30-15.ext_restart
*Output sent to file c30-15.ine
*Totals: facets=341088 bases=319770
*Dictionary Cache: max size= 15 misses= 0/319769 Tree
Depth= 14
*52.359u 1.046s 4320Kb 1125 flts 0 swaps 0 blks-in 0 blks-out
In this case neither 64-bit or 128-bit precision is enough so lrsgmp was used for the computation.
Estimation
The estimation feature of lrs allows estimates to be
made of the output size and running time. These are based on
Knuth's technique for estimating the size of backtracking trees,
and are described in Avis
and Devroye(1994). The estimate is unbiased, that
is the expected value of the estimate is the actual value. To
get an estimate use the maxdepth
option to limit the search depth, and the estimates option:
maxdepth d
estimates k
This will cause lrs to perform k random probes from
each node of the tree at depth d. k should be at least 1
and d at least zero.
(New in V6.0) In order to try to
get a better estimate, we implemented the additional option which
makes the search go deeper than maxdepth
when the estimates are large.
subtreesize n
(default is MAXD)
If an estimate obtained for a subtree at depth d exceeds n then
the estimation is continued deeper into that subtree until an
estimate less than or equal to n is obtained.
The
running time of lrs is proportional to the number of
bases, so an estimate of the number of bases gives an easy way to
estimate the running time for solving the complete problem by lrs:
total running time =
time for estimate * estimated number of bases / tree nodes
evaluated.
H-representation: If the input is an
H-representation, the program gives an unbiased estimate of
the number of vertices and rays in the
V-representation, and the total number of bases that
will be computed by lrs. For the H-representation cube.ine,
the options maxdepth 1 and
estimates 1 produce the
output:
*Estimates:
vertices=9 rays=0
bases=9
*Total number of tree nodes
evaluated: 6
*Estimated total running
time=0.0 secs
In this case the V-representation of the cube
is estimated to have 9 vertices, and it is estimated that lrs
will compute a total of 9 bases. The estimate was based on
evaluating 6 tree nodes. Note: The estimate for
the number of rays may be an overestimate if the polyhedron is
not a cone, since some rays may be duplicated in the output -
see subsection Output
Duplication.
V-representation: If the
input is a V-representation, the program gives an unbiased
estimate of the number of facets in the H-representation, and
the total number of bases that lrs will compute.
For V-representation cube.ext, the options maxdepth 0 and estimates 3 produce the
output:
*Estimates: facets=6 bases=7 volume=8.88889
*Total number of tree
nodes evaluated: 10
*Estimated total
running time=0.0 secs
In this cases it is estimated that the H-representation of the
cube will contain 7 facets, and it is estimated that lrs
will compute a total of 7 bases to find it.
An unbiased estimate of the volume of the polytope is also
given. The estimate was formed by evaluating 7 tree
nodes.
Voronoi diagrams: Estimates for the number of Voronoi
vertices and Voronoi rays for a V-representation of a set of
data points may be obtained by combining the voronoi, estimates and maxdepth options.
Repeated estimates: In order to get estimates with
different random probes, lrs can be given a seed for
the random number generator
by the seed option.
seed n
The integer n is used as a seed for the
random number generator.
Using the estimator: For the case of polytopes that
contain the origin, a V-representation can be processed as an
H-representation and vice-versa (this is an application of
duality). Hence facet estimates for a V-representation can also
be obtained by running the problem as an H-representation with
the estimates option. The estimated number of vertices will be
in this case be an unbiased estimate for the number of facets
for the original problem.
Since the origin is an interior point, the
estimated number of vertices is an accurate estimate of the
number of facets of the H-representation of the
cube. Similarly, estimates for an input
H-representation of a polytope containing the origin may be
obtained by processing the file as a V-representation. The
output will be essentially the same, but the number of bases
computed may be very different, see the subsection H- vs
V-representation. For a large problem of
this type, it is useful to get estimates for the number of bases
that lrs will compute for both V- and H-representations,
so that simpler problem can be chosen.
The estimates may also be used to judge the feasibility of
solving the problem using other codes. For example, any code
that uses triangulation/perturbation to resolve degeneracy
will have trouble if the number of bases is huge. Codes which
must store all the output in memory (currently all codes
except reverse search methods such as lrs) will have
trouble if the estimated output size is huge.
mplrs: installation and usage
C wrapper prepared by Skip Jordan for lrs
that allows for parallelization using the MPI library over a
network of multi-core machines. It is derived from plrs but includes many
modifications to ensure load balancing. Near linear speedups up to
1200 cores have been observed.
New in v7.2: mplrs can compute
a minimum representation in parallel, see -minrep option below and minrep.
Default installation (see below for more
details):
% make mplrs
(compilers with __int128
support)
or
% make mplrs64
(otherwise)
As with lrs, this produces binaries mplrs
using hybrid (64bit/128bit/GMP) arithmetic and mplrsgmp which uses only GMP
arithmetic
See arithmetic packages to see
how to get single arithmetic versions mplrs1, mplrs2(if
__int128 supported)
Default usage: <number of processes> should be
4 or higher
% mpirun -np <number of processes> mplrs
<infile> [ <outfile> ] (See below for all mplrs options)
Note: Remove all options after the end statement of the input file!
Example: Input file mp5.ine is run
with 8 processors. The output file mp5.mplrs is in the
distribution.
This produced 378 subtrees that were enumerated in parallel using
6 producer cores, 1 core controlling the run and 1 core
collecting the output.
mai20% mpirun -np 8 mplrs mp5.ine mp5.mplrs
*mplrs:lrslib v.6.0 2015.7.13(lrsgmp.h)8 processes
*Copyright (C) 1995,2015, David Avis avis@cs.mcgill.ca
*Input taken from mp5.ine
*Output written to: mp5.mplrs
*Starting depth of 2 maxcobases=50 maxdepth=0 lmin=3 lmax=3
scale=100
*Phase 1 time: 0 seconds.
*Total number of jobs: 378, L became empty 4 times
*Totals: vertices=32 rays=0 bases=9041 integer-vertices=16
*Elapsed time: 1 seconds.
2.285u 0.137s 0:01.86 129.5% 0+0k 0+9976io
36pf+0w
Installation instructions for mplrs.
1. Install MPI library on all machines that will be used for a
single run. We have tested mplrs with both openmpi
and mpich2. Note that if you
install MPI from binary packages, you will need both the library
and development packages if available. Configuring MPI to run on a
cluster of machines is beyond the scope of this document, however
mplrs should work well on any
properly-configured cluster or supercomputer.
2. Make any path changes to the beginning of makefile as necessary.
3. Run %make mplrs
As with lrs, this
produces binaries mplrs
using hybrid (64bit/128bit/GMP) arithmetic and mplrsgmp which uses only GMP arithmetic
4. Exactly the same version
of mplrs must be used on each
machine in the cluster, or unexpected results may occur!
5: mplrs creates temporary
files on each machine in the cluster. The default is to use /tmp.
If this is not writeable the -temp
option must be used, see below.
Full
set of options for mplrs
mplrs has many options, but just using the
default settings should provide good performance in general.
The parameters -hist and -freq give interesting information about
the degree of parallelization.
mpirun -np <number of processes> mplrs <infile>
<outfile> -id <initial depth> -maxc <maxcobases>
-maxd <depth> -lmin <int> -lmax <int> -scale
<int> -hist <file> -temp <prefix> -freq
<file> -stop <stopfile> -checkp <checkpoint
file> -restart <checkpoint file> -time <seconds>
-np <number of processes> required, should be at least 4
default
-id <initial
depth>
2
the depth of the original tree search to
populate the job queue L
-maxc
<maxcobases>
50 (*scale)
a producer stops and returns all subtrees
that are not leaves to L after generating maxc nodes
-maxd
<depth>
0
a producer returns all subtrees that are not
leaves at depth maxd. Zero if not used
-lmin <int>
3
if job queue |L|<np*lmin then the maxd parameter is
set for all producers
-lmax
<int> lmin
if job queue |L|>np*lmax then then maxc
is replaced by maxc*scale
-scale
<int>
100
used by lmax
-hist
<file>
store parallelization data in <file>
for use by gnuplot, see below
-temp <prefix>
/tmp/
store a
temporary file for each process. Should be specified if /tmp not
writeable.
Using " -temp ./
" will write temporary files to the current directory
-freq
<file>
store frequency
data in <file> for use by gnuplot, see
below
-stop <stopfile>
terminate mplrs if a file with name
<stopfile> is created in the current directory
-checkp <checkpoint
file>
if mplrs is terminated by -stop or -time
then it can be restarted using this <checkpoint file> and
-restart
-restart <checkpoint
file>
restart mplrs using previously created
<checkpoint file>. If used with
-checkp file names should be different!
-time
<seconds>
terminate mplrs after <seconds> of
elapsed time
New in V6.2:
-countonly
don't output vertices/rays/facets, just
count them
-maxbuf
<n>
500
controls maximum
size of worker output buffers
smaller values
increase "streaminess" of the output while larger values send
larger blocks of output
-stopafter
<n>
exit after
approximately <n> cobases have been computed (no guarantee
about how many vertices/rays/facets computed)
New in V7.3:
-minrep
find a minimum representation of the input file ( see minrep )
-fel
do one iteration of Fourier-Motzkin elimination and
remove redudancies in parallel ( see Fourier-Motzkin )
Checkpoints, restarts
and abnormal termination
mplrs has inherited restart
capability from lrs, which was described in Timing
and interrupts
Details of the layout of the checkpoint file can be found here.
Checkpointing can be very useful for long runs that use
significant computational resources. If resources are needed
elsewhere, or additional resources become available, it is
possible to stop mplrs and use the checkpoint file to restart. The
mpirun command can be modified for this restart to reflect the new
resource availability. The normal way to do this by using the
-checkp and either the -stop or -time options. In addition if
mplrs receives a SIGTERM or SIGHUP signal, it checkpoints and
terminates. This allows users to checkpoint runs that were
not started with -stop <file> or -time
<seconds>. These signals can be sent using the kill
utility:
% kill <pid>
where <pid> is the process ID of an mplrs instance to be
terminated.
Sending the signal to any one of the mplrs instances is
sufficient.
The checkpoint is produced in the file specified by the -checkp
argument. If it was not specified,
the checkpoint is produced in the output.
In this case, the checkpoint file is contained between the lines
*Checkpoint file follows this line
and
*Checkpoint finished above this line .
These two lines are not part of the checkpoint file.
To terminate the run immediately, without a checkpoint, use
% kill -9 <pid>
Visualization of parallelization
A good
realtime view of an mplrs run can be obtained by using the
-hist and -freq parameters and gnuplot using the plotL.gp and
plotD.gp files.
These
files can be used if the parameters are set as -hist
hist -freq freq and can be obtained while mplrs
is running as follows:
%gnuplot plotL.gp
%gv plotL.ps
%gnuplot plotD.gp
%gv plotD.ps
If other files are used for -hist and -freq then plotL.gp
and plotD.gp should be edited accordingly.
The first plot has 3 graphs showing the number of
processors working, the size of the job queue L, and
message requests pending, all versus elapsed time on the
x-axis.
The second histogram shows the size of the subtrees
explored by producers. The root of the subtree is not
counted in this size. Note that a producer stops after
maxc nodes are explored, but in backtracking some
additional leaves may be discovered. So the size of the
largest subtree maybe slightly larger than maxc.
Details of -hist and -freq files
mplrs periodically adds a line to the histogram file, for
example
54.118141 94 279 94 0 0 373
This line contains the following information:
Time since execution began in seconds
(54.118141 here)
Number of busy workers (94 here)
Current size of job queue (279 here)
Number of workers that may return unfinished
jobs (94 here)
Unused (0 here)
Unused (0 here)
Total number of jobs that have been in the
job queue (373 here)
The second and fourth entries are similar and can differ
due to
latencies.
The frequency data file contains one integer per line,
with each integer
corresponding to the size of a subtree explored by a
worker.
Fourier Elimination (fel
mode)
(new in v7.2, lrs/mplrs)
Compute the projection of a
polyhedron given by its
H-representation
onto a selected set of coordinates.
This function is invoked by either the clone fel of lrs, or by
lrs itself if these options are included at the
end of the input file.
project k i1 i2
... ik
// project onto coordinates
k i1
i2 ... ik
eliminate k i1 i2
... ik
// eliminate coordinates
k
i1 i2 ... ik
An lrs format H-representation is produced.
mplrs will compute a projection using parallel redundancy removal
and can be invoked by mplrs -fel. The input needs to have
no hidden linearities. mplrs will test for this and produce
a minimum representation if any are present. This file can
be rerun to perform the projection.
If no options are present fel or mplrs -fel will project out the last
coordinated of the input file.
mplrs will only project/eliminate one variable. To
project/eliminate all variables run multiple times or use the
mfel shell script.
project/eliminate for a
V-representation
is a much simpler operation which involves extracting the given
columns and removing redundancies. It is not implemented in mplrs.
lrsnash installation and usage (Nash
equilibria for 2-person matrix games)
See: D.
Avis, G. Rosenberg, R. Savani, B. von Stengel, "Enumeration of Nash Equilibria for
Two-Player Games", Economic
Theory 42(2009) 9-37 pdf
lrsnash computes
all Nash equilibria (NE) for a two person noncooperative game
are computed using two interleaved reverse search vertex
enumeration steps.
The input for the problem are two m by n matrices A,B of
integers or rationals. The first player is the row player, the
second is the column player.
If row i and column j are played, player 1 receives Ai,j
and player 2 receives Bi,j.
Version 6.1 contains lrsnash.c and
lrsnashlib.c replacing nash.c with a library version and simpler
interface that does not require setupnash.
Big thanks to Terje Lensberg for this.
nashdemo.c is a very basic template for setting up games and
calling the library function lrs_solve_nash(game *g).
To compile:
% make lrsnash
you get binaries
lrsnash, lrsnash1,
lrsnash2, nashdemo and
2nash.
The first three are variants of lrsnash that use different
arithmetic packages.
lrsnash uses gmp
arithmetic and will work with any input files.
lrsnash1 uses 64-bit
arithmetic with overflow checking and is about 5-10 times faster
than
lrsnash for
combinatorial game matrices.
lrsnash2 uses 128-bit arithmetic
where available and takes about about 50% more time than
lrsnash1.
% nashdemo
just runs the demo, no parameters
% lrsnash game
finds the equlibrium for file
game
[
% lrsnash game1 game2
or % 2nash game1 game2
finds the equilibrium for
game1 and
game2 in
legacy nash format which is described below ]
The file
game is in the format :
m n
matrix A
matrix B
eg. the file
game is for a game with m=3 n=2:
3 2
0 6
2 5
3 3
1 0
0 2
4 3
% lrsnash game
*Copyright (C) 1995,2015, David Avis
avis@cs.mcgill.ca
*lrsnash:lrslib v.6.1 2015.10.27(lrsgmp.h gmp v.6.0)
2 1/3 2/3 4
1 2/3 1/3 0 2/3
2 2/3 1/3 3
1 0 1/3 2/3 8/3
2 1 0 3
1 0 0 1 4
*Number of equilibria found: 3
*Player 1: vertices=5 bases=5 pivots=8
*Player 2: vertices=3 bases=1 pivots=8
*lrsnash:lrslib v.6.1 2015.10.27(32bit,lrsgmp.h)
------------------------------------------------------------------
Output interpretation:
Each row beginning 1 is a strategy for the row player yielding a
NE with each row beginning 2 listed immediately above it.
The payoff for player 2 is the last number on the line beginning
1, and vice versa.
Eg: first two lines of output: player 1 uses row probabilities
2/3 2/3 0 resulting in a payoff of 2/3 to player 2.
Player 2 uses column probabilities 1/3 2/3 yielding a payoff of
4 to player 1.
Legacy format
% setupnash game game1 game2
produces two H-representations, game1 and game2, one for each
player.
To get the equilibrium, run
% lrsnash game1 game2
If you have two or more cpus available run
2nash instead of
lrsnash as the order of the
input games is immaterial.
It runs in parallel with the games in each order.
(If you use lrsnash, the
program usually runs faster if m is <= n , see below.)
% 2nash game1 game2 [outputfile]
If no output file is specified the output is placed in a file
names
out.
If
both matrices
are
nonnegative and
have
no zero columns,
you may instead use
setnash2:
% setnash2 game game1 game2
Now the polyhedra produced are polytopes.
The output of lrsnash in this case is a list of unscaled
probability vectors x and y.
----------------------------------------------------------
% lrsnash game1 game2
Processing legacy input files. Alternatively, you may skip
setupnash and pass its input file to this program.
*nash:lrslib v.6.1 2015.10.27(lrsgmp.h gmp v.6.0)
*Copyright (C) 1995,2015, David Avis
avis@cs.mcgill.ca
*Input taken from file game1
*Second input taken from file game2
***** 4 3 rational
2 1/12 1/6
1 1 1/2 0
2 2/9 1/9
1 0 1/8 1/4
2 1/3 0
1 0 0 1/4
*Number of equilibria found: 3
*Player 1: vertices=6 bases=6 pivots=8
*Player 2: vertices=4 bases=1 pivots=8
*nash:lrslib v.6.1 2015.10.27(32bit,lrsgmp.h)
-----------------------------------------------------------
To normalize, divide each vector by v = 1^T x and u=1^T y.
u and v are the payoffs to players 1 and 2 respectively.
If m is greater than n then
lrsnash
usually runs faster by transposing the players. This is achieved
by running:
% lrsnash game2 game1
If you wish to construct the game1 and game2 files by hand, they
are fragile and should be done exactly as follows:
For player 1: eg. game1
One linearity in the last row
Identity matrix with additional final column 0
Transpose of payoff matrix for player 2 with final
column 1
Last row is prob sum to one
For player 2: eg. game2
One linearity in the last row
Payoff matrix for player 1 with final column 1
Identity matrix with additional final column 0
Last row is prob sum to one
Corresponding to file game above we get
*game: player 1
H-representation
linearity 1 6
begin
6 5 rational
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 -1 0 -4 1
0 0 -2 -3 1
-1 1 1 1 0
end
*game: player 2
H-representation
linearity 1 6
begin
6 4 rational
0 0 -6 1
0 -2 -5 1
0 -3 -3 1
0 1 0 0
0 0 1 0
-1 1 1 0
end
Linear
Programming
lrs can be used to solve linear programming problems in
rational arithmetic when the input is an H-representation.
Use the option:
lponly
and
one
of the options maximize or minize:
maximize
a0 a1 ... an-1
//
H-representation
only //
simply maximizes the function a0 + a1
x 1 + ... + an-1 xn-1
over the given polyhedron. A optimal vertex is given when
it exists, otherwise for unbounded solutions a vertex and ray is
given. A minimization will be performed if the following
option is specified:
minimize a0
a1 ... an-1
//
H-representation
only //
To print the dictionary at a few key points also include the
option:
verbose
New
in
V4.2. Dual variables are now printed at
termination. If the linearity option is used, only a partial
list of dual variables will be given.
Dual
variable
yi refers to inequality number i in the input.
Volume and triangulation
lrs can be used to compute the volume of a full dimensional polytope given as a
V-representation. This follows from the fact that lex-postive
bases form a triangulation of the facets, and that a
V-representation is always lifted. See "Theoretical Description"
on lrs home page for some remarks on this. The option
volume
//
V-representation
only //
will cause the volume to be computed. For input cube.ext, the
output is:
*Volume=8
The triangulation can be output by adding also the option verbose.
This would give the output:
F#0 B#1
h=0 vertices/rays 4 6 7 8 I#8 det= 8
1
1
0 0
1
0
1 0
1
0
0 1
F#3 B#2
h=1 vertices/rays 4 5 6 7 I#8 det= 8
F#3 B#3
h=2 vertices/rays 3 4 5 7 I#8 det= 8
1
-1 0 0
F#4 B#4
h=3 vertices/rays 2 3 4 5 I#8 det= 8
1
0
0 -1
F#5 B#5
h=4 vertices/rays 1 2 3 5 I#8 det= 8
F#5 B#6
h=2 vertices/rays 2 4 5 6 I#8 det= 8
1
0 -1 0
end
*Sum of
det(B)= 48
*Volume=
8
Each of the 6 bases corresponds to a simplex.
The first simplex is composed of vertices 4 6 7 8, second
simplex is 4 5 6 7, etc.
If the volume option is
applied to an H-representation, the results are not predictable.
If the option is applied to a V-representation of a
polytope that is not full dimensional, the volume of a projected
polytope is computed. The projection used is to the
lexicographically smallest coordinate subspace, see Avis,
Fukuda, Picozzi (2002).
For polytopes given by a H-representation, it will first be
necessary to compute the V-representation.
Voronoi diagrams and Delaunay triangulations
lrs can be used the compute the V-vertices of a Voronoi
diagram of a set of data points in n-1 dimensional space. To do
this we use a standard lifting procedure (see, e.g., Edelsbrunner,
"Algorithms in Combinatorial Geometry," pp 296-297) . Each point
is mapped to a half space tangent to the parabaloid in n
dimensions, by the mapping:
p1 , p2 , ...., p n-1
-> (p1 2 +
p22 + ... + pn-12
) - 2 p1 x 1 - 2 p2
x2 - .... - 2 p n-1 xn
-1 + x n>= 0
lrs is applied to the H-representation so created.
This transformation is performed automatically for a
V-representation if the
voronoi
// V-representation only - place
immediately
after end statement //
option is specified.
Note: The input file must consist entirely of data points
(no rays), i.e.. there must be a one in column one of each line.
The volume option should
not be used, since the volume reported will not be the volume of
the original V-representation.
The output will consist of the Voronoi vertices (columns
beginning with a one) and Voronoi rays (columns beginning with
zero) for the Voronoi diagram defined on the data points.
If the printcobasis option
is given, the n "data points"
indices produced will tell which set of input data points
corresponds to the given Voronoi vertex or ray. In case of
degeneracies, a given Voronoi vertex may be generated by more
than n of the input data points. In this case, use of the allbases option will cause
all sets of n input data points corresponding to a Voronoi
vertex to be printed. Each cobasis will define a Delaunay triangle in the dual.
For Voronoi rays, the immediately preceding cobasis is the
cobasis of the the Voronoi vertex from which the ray
emanates. The index followed by a * is
the data point to drop in order to generate the ray. If the geometric option is given the
correspondence between Voronoi rays and Voronoi vertices will be
produced automatically.
Example: Compute the
Voronoi diagram and Delaunay triangulation of the planar point
set (0,0), (2,1), (1,2), (0,4), (4,0), (4,4) (2,-4).
Input:
vor7-3.ine
*6 Voronoi
*7 input data pointV-representation
begin
7 3 integer
1 0 0
1 2 1
1 1 2
1 0 4
1 4 0
1 4 4
1 2 -4
end
voronoi
printcobasis
allbases
geometric
Run:
% lrs vor7-3.ine
|
Output:
V-representation
begin
***** 3 rational
V#1 R#0 B#1 h=0 data points 1 5 7 det=64
1 2 -3/2
V#1 R#1 B#1 h=0 data points 1 5* 7 det=64
0 -2 -1
V#1 R#2 B#1 h=0 data points 1* 5 7 det=64
0 2 -1
V#1 R#2 B#2 h=1 data points 1 2 5 det=16
1 2 -3/2
V#2 R#2 B#3 h=2 data points 1 2 3 det=12
1 5/6 5/6
V#3 R#2 B#4 h=3 data points 1 3 4 det=16
1 -3/2 2
V#3 R#3 B#4 h=3 data points 1 3* 4 det=16
0 -1 0
V#4 R#3 B#5 h=2 data points 2 5 6 det=32
1 15/4 2
V#4 R#4 B#5 h=2 data points 2* 5 6 det=32
0 1 0
V#5 R#4 B#6 h=3 data points 2 3 6 det=20
1 27/10 27/10
V#6 R#4 B#7 h=4 data points 3 4 6 det=32
1 2 15/4
V#6 R#5 B#7 h=4 data points 3* 4 6 det=32
0
0 1
end
|
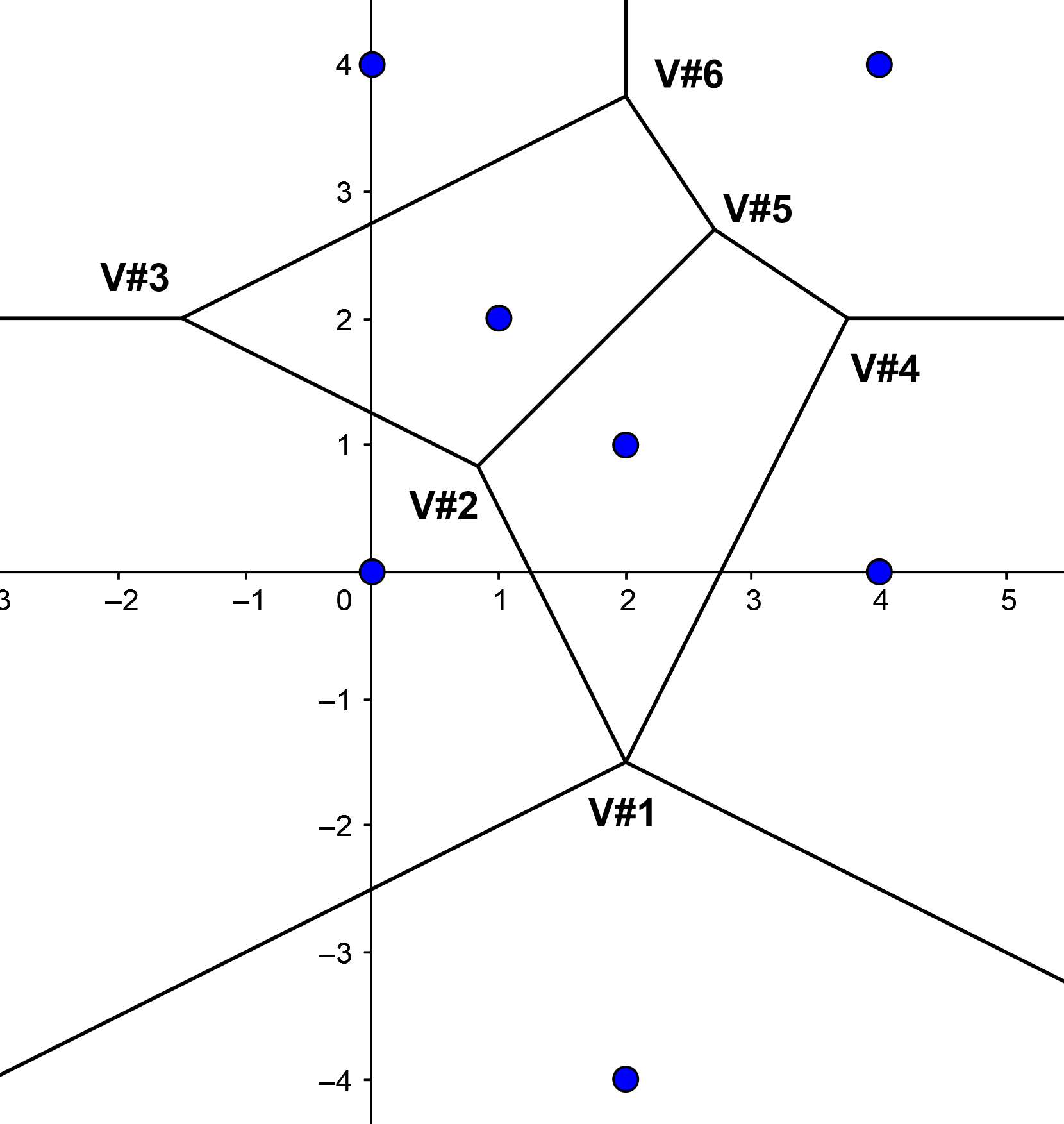
Voronoi diagram: Blue circles
mark input data points, Voronoi diagram in black
6 Voronoi vertices: (2, -3/2),
(5/6,5/6),(-3/2,2),(15/4,2), (27/10,27/10), (2,15/4).
The Voronoi vertex (2,-3/2)
appears twice in the output with data point indices 1
5 7 and 1 2 5. This means that it is degenerate and is
defined by the set of 4 input data point in positions
1,2,5,7 in the input file. I.e.. it is the centre of
an empty circle through the four input data
points (0,0), (2,1), 4,0), (2,-4). The
other Voronoi vertices appear once each and are defined
respectively by the data points with
indices (i.e.. position in the input file)
1 2 3, 1 3 4, 2 5 6, 2 3 6 and 3 4
6. The Voronoi diagram has 5 rays
(2, -3/2) +
(-2t,-t),
(2,-3/2)+(2t,-t),
(-3/2,2)+(-t,0),
(15/4,2)+(t,0), (2,15/4)+(0,t)
For
example, the first ray in the output appears:
V#1 R#1 B#1 h=0 data points
1 5* 7 det=64
0 -2 -1
This means that the ray
(-2t,-t) emanates from the vertex V#1 defined by data
points 1 5 7, namely (2, -3/2). The asterisk on index 5
indicates that the ray is defined by the data points
with indices 5 and 7, namely (0,0) and (2,-4). |
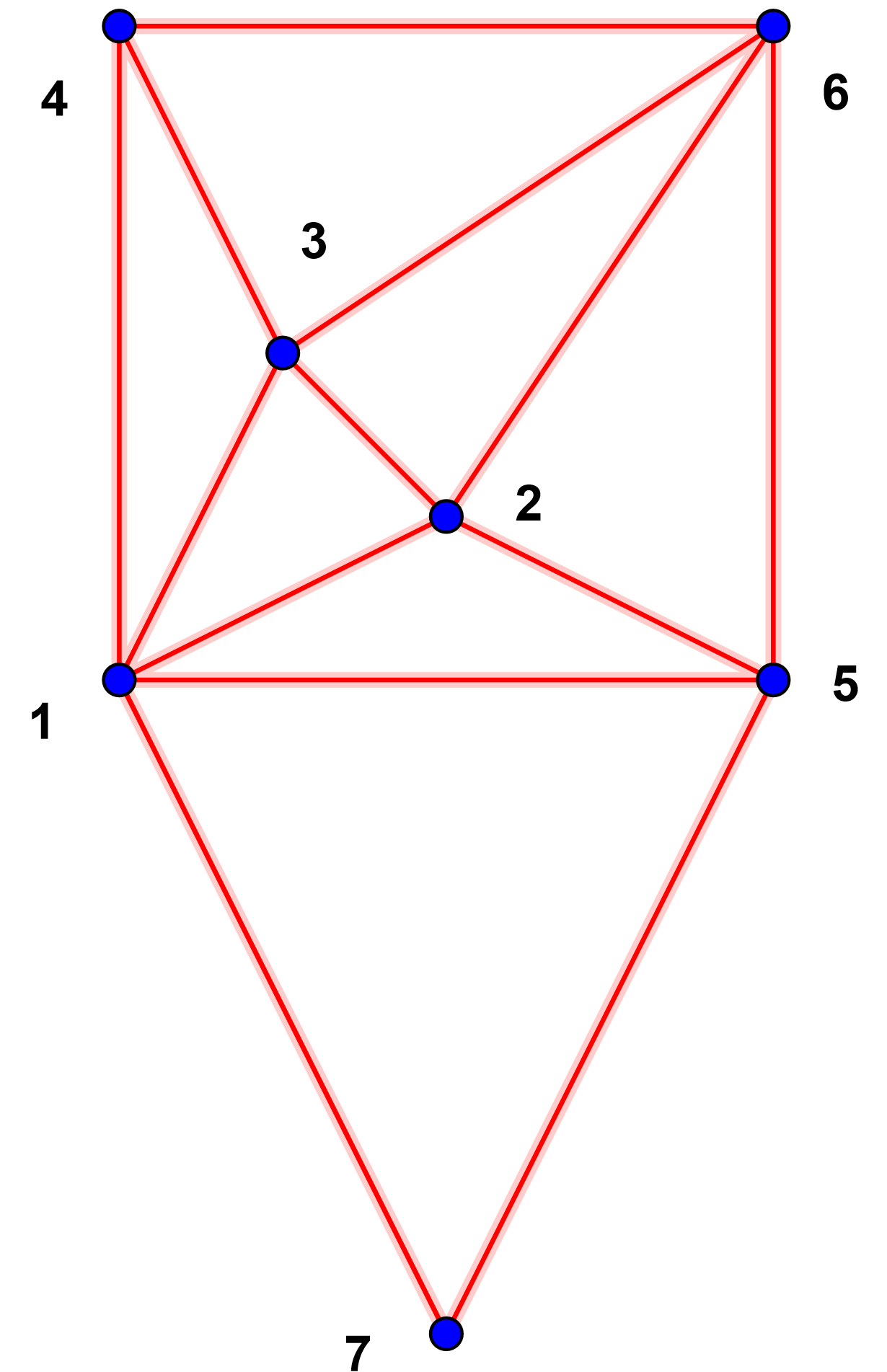
Delaunay triangulation Blue
circles mark input data points, Delaunay
triangulation in red.
Each of the 7 cobases defines a triangle in the dual:
157, 125, 123, 134, 256, 236, 346
Here each index refers to the line number of the data
point in the input file.
Eg. 157 describes the triangle (0,0),(4,0),(2,-4)
|
Visualizations made using GeoGebra.
redund: extreme point enumeration
and eliminating redundant inequalities (new options parallel version from
v7.1)
minrep: finding a minimum representation of
an H- or V-representation
(new options parallel version from
v7.3)
A convex hull problem that occurs frequently is to enumerate the
extreme points (vertices) of a given set of input points. This
problem is in fact much simpler than the problem of finding the
facets of the given input point set. It can be solved by linear
programming. The dual problem is to remove redundant
inequalities from an H-representation. An input inequality
is redundant if it can be deleted without changing the polyhedron.
It is strongly redundant if it is not satisfied as strict inequality
by any feasible point. A vertex/ray in a V-representation
is strongly redundant if it is strictly interior to the convex hull.
An H-representation may contain "hidden linearities" or
inequalities that are always satisfied as equations. A similar
situation occurs in a V-representation where the convex hull
contains a line. The minimum representation problem is to identify
all linearities in an input file, output them explicity using the
linearity option, and then remove any remaining redundant rows.
The dimension of the input set is output at the end of the computation.
Redundancy removal can be obtained by using the lrs clone redund
or by lrs via the redund/redund_list options
described above.
A minimum representation can be obtained by using the lrs clone minrep
or by lrs via the testlin (before the begin line)
and redund/redund_list options.
mplrs can compute a minimum representation in parallel
by use of the -minrep command line argument. Due to technical issues
in the parallelization mplrs does not do redundancy removal
without also computing a minimum representation.
The ouput will be streamed if the verbose
option is included after the end
line.
On each line *nr indicates
non-redundant, *re indicates
redundant,
*sr indicates
strongly redundant,
and *li indicates
linearity.
Usage:
(1) With options
(allows partial redundancy checking for large inputs)
Add the redund or redund_list
option after the end statement of a H- or V-representation.
Execute % lrs filename
or %mpirun -np <procs>
mplrs filename
If more than one redund/redund_list option is in the input file
the last one read takes priority.
(2) Without options
(complete redundancy check of all input lines, overidden by redund/redund_list option in input)
To remove input lines that are not vertices/rays from a
V-representation or redundant inequalities from an
H-representation use the command:
% redund filename
or
% mpirun -np <procs> mplrs -minrep
filename
For example, using the file mit.ine from the
distribution:
% redund mit.ine
*redund:lrslib v.7.1
2020.5.23(64bit,lrslong.h,overflow checking)
*Input taken from file mit.ine
mit.ine
*mulint : max(|a|,|b|) > 2147483647
*redund2 found - restarting
*redund:lrslib v.7.1 2020.5.23(128bit,lrslong.h,overflow
checking)
*Input taken from file mit.ine
mit.ine
*row 75 was redundant and removed
*row 77 was redundant and removed
*row 89 was redundant and removed
--------------------------
*row 709 was redundant and removed
H-representation
begin
708 9 rational
36 0 0 -2 -2 -1 0 0 0
----------------------------
0 0 0 0 0 0 0
0 1
end
*Input had 729 rows and 9 columns: 21 row(s) redundant
*Overflow checking on lrslong arithmetic
*redund:lrslib v.7.1 2020.5.23(128bit,lrslong.h)
From this output we
first see that redund tried 64 bit arithmetic but detected an
overflow and reran with 128 bit arithmetic.
It found 21 redundant rows which were removed from the file.
The resulting output file can be used directly with lrs.
In fact, lrs works best if the input is non-redundant, see the
section Redundancy vs
Degeneracy.
Linearities
linearity k i1 i2
i ... ik
The input file contains k linearities. If the input is
a H-representation, the rows i1
i2 i ... ik of the input
file are equations. For a V-representation, the rows with these
indices should begin with zero in column one, and will be
interpreted as lines rather than rays. Linearities defined
on the input vertices of a V-representation are not defined, but
the program will accept them and produce some output. Each of
the indice ik
must be a distinct number between 1
and m. With an
H-representation, linearities are useful for enumeration of
vertices on a facet or lower dimensional subspace. For example
the file:
cube_ridge
*cube of side 2 centred at the origin
H-representation
linearity 2 1 5
begin
6 4 rational
1 1 0 0
1 0 1 0
1 0 0 1
1 -1 0 0
1 0 -1 0
1 0 0 -1
end
causes vertices to be enumerated on the
ridge which is the intersection of the two facets
x1 = -1
and x2 = 1
so the output is the pair of vertices
cube_ridge
*Input linearity in row(s) 1 5
V-representation
begin
2 4 rational
1 -1 1 1
1 -1 1 -1
end
Specifying linearities in this way will often produce redundancy , especially
if the dimension of the problem is reduced considerably. As a
preprocessing step, it is useful to apply to remove any
redundancy by redund. In the
case of the above problem the output produced by redund
is:
cube
*Input linearity in row(s) 1 5
*row 2 was redundant and removed
*row 4 was redundant and removed
H-representation
linearity 2 1 2
begin
4 4 rational
1 1 0 0
1 0 -1 0
1 0 0 1
1 0 0 -1
and two redundant halfspaces were
removed.
Redundant columns are closely related
to linearities. If we examine the V-representation of
cube_ridge above we can see that it is just a line segment
in 3 dimensional space. Further, columns 2 and 3 are
multiples of column 1. If lrs is applied to this file, the
column redundancies give rise to two linearities, so the
output will appear as the H-representation given above:
geometrically the intersection of two planes (the
linearities) with two half-planes (defining the endpoints of
the line segment).
In general, the representation of the
linearity space is not unique, however the one produced by
lrs should be the same as that produced by cdd.
lrs timing and
interrupts
(for mplrs see
here)
lrs handles certain signals unless it is compiled with the
-DSIGNALS option. It is possible to interrupt lrs and
get the latest cobasis, which can be used for restarting the
program (useful if the machine is going down!)
signal
operation
USR1
print
current
cobasis and continue
TERM
print
current
cobasis and terminate
INT
(ctrl-C)
ditto
HUP
ditto
lrs also provides timing information unless it is compiled with
the option -DTIMES.
For example, when hitting CTL-C when running
%lrs mit.ine
the following is obtained:
....
1 24 48 0
0 0 0 64 0
1 24 48 0
0 0 0 72 0
lrs_lib: checkpointing:
lrs_lib: State #0: (LRS globals)
restart 33 0 12542 8
634 640 641 678 704 725 726 729
integervertices 14
lrs_lib: checkpoint finished
4.476u 0.000s 0:04.49
99.5% 0+0k 0+0io 5657pf+0w
The restart and integervertices lines can be used to restart by
adding them to the end of the mit.ine file:
0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 1
end
restart 33 0 12542 8 634 640 641 678 704 725
726 729
integervertices 14
Now
% lrs mit.ine
*lrs:lrslib v.7.0
2018.6.14(64bit,lrslong.h,hybrid arithmetic)
*Input taken from mit.ine
mit.ine
*restart V#33 R#0 B#12542 h=8 facets 634 640
641 678 704 725 726 729
*lrs:overflow possible: restarting with 128
bit arithmetic
1 16 16 8
2 1 4 32 8
1 16 80/3 16/3
0 0 0 64/3 0
1 21 18 9/2
3/2 0 0 24 6
....
will complete the full run.
hvref/xref
Cross reference listing between V- and H-representations
(new in v7.1)
This standalone hvref/xref makes a cross reference list between H
and V representations.
The first step is to create a matching pair of representations using
lrs/mplrs.
(The same steps can be used starting with a V-rep *.ext file)
First it is recommended to remove any redundancies from the input
file using redund.
1. Add printcobasis and incidence options to cube.ine
% lrs cube.ine cube.ext
or %mpirun -np <procs>
mplrs cube.ext
% xref cube.ext
2. Edit the output file cube.ext.x to insert a second line
that contains two integers
rows maxindex
where rows >= # output lines in cube.ext.x
maxindex >= # input lines in
cube.ine
or just use 0 0 and run as below, the output will tell you which
values to use
% hvref cube.ext.x
Testing redundancy in
projections
Given a polyhedron
with
H-representation
,
the projection of onto the
variables can be given by an
H-representation ,
where
if
and only if there is some
such that
.
can be
computed by lrs/mplrs in fel
mode by using the project/eliminate
options.
Let
be the
-th
inequality in the H-representation of P.
This inequality
is redundant in the computation of
the projection if and only
if deleting it does not change the projection.
This redundancy can be tested by computing the two projections and
comparing them, a potentially very long computation.
lrslib contains an alternative way of testing this redundancy
directly by use of an SMT solver without computing the projections
directly.
This requires that an SMT solver such as z3
or cvc4
be installed.
projred
is a script for performing this operation on one or more
inequalities in an H-representation for
polyv
is a C program for computing an SMT file to verify the redundancy
of an inequality in computing a projection of
Error messages and
troubleshooting
The most common error occurs from an incorrect input file
specification, please check the section File
Formats carefully. In particular, lrs does not
check the type or number of input coefficients specified.
After the line
m n rational
you must specify exactly m*n
rational or integer coefficients. They are read in free
format , but normally each input facet or vertex/ray is
begun on a new line. See note for cdd users.
The following error messages are produced by lrs . They
are arranged in alphabetic order.
Cannot find linearity in the basis
The linearity option was specified but a basis cannot be
created. Check the linearity indices are all less than n-1 and
are disitinct.
Data type must be integer of rational
lrs does not handle floating point
data, change to integer or rational input.
Digits must be at most 2295 Change
MAX_DIGITS and recompile
(This message does not appear if the default gmp arithmetic
package is used)
The digits option was specified, but the
number of decimal digits is too large (the values shown
here is for 64 bit machines). MAX_DIGITS (default 255)
is the maximum number of array locations used for extended
precision arithmetic. This value should be increased and
lrs recompiled.
Invalid input: check you have entered
enough data!
Usually
means that end of file was reached before enough input data
was read.
Invalid Co-basis - does not have correct rank
An attempt to restart from an invalid
cobasis has been made. Check that the indices are entered
exactly as they appear in the previous aborted run.
Maximize/minimize only valid for
H-representation
LP operations can only be performed on
H-representations.
No begin line
No data in file
No feasible solution
The input is an H-representation of an
infeasible system.
Starting cobasis indices must be distinct
and in range 1 .. m
The startingcobasis option has been used,
but the indices supplied were not valid: i.e. distinct numbers
between 1..m.
Trying to restart from infeasible
dictionary
An attempt to restart from an invalid
cobasis has been made. Check that the indices are entered
exactly in the order appear in the previous aborted run.
mplrs error messages
Error: lponly option not supported - use
lrs!
The simplex method does not run in
parallel
The following message may be produced when building lrs on macOS
OpenMP support not found, disabling OpenMP parallel build
Apple's Xcode compilers do not support OpenMP, so the build
produced a single-threaded lrs. Multithreaded lrs can be built
on macOS using e.g. gcc from MacPorts.
Hints and comments
H- vs V- representation
lrs is programmed to manipulate
H-representations directly. A file presented as a
V-representation is processed by lifting it to a cone in one
higher dimension, which is treated internally as a
H-representation. If the input file is a polytope which contains
the origin, then the user has two options. Submit it as a
V-representation and have it processed as just described, or
submit it as a H-representation, and interpret the output as a
list of facet inequalities rather than "vertices". Since this
will not be lifted, it will be processed in a different way by lrs.
Sometimes a degenerate V-representation may run more quickly as
a H-representation, and sometimes more slowly. To decide which
representation to use for a large problem, the user can run the
estimates option and choose the representation with
fewest estimated bases.
Redundancy vs Degeneracy
For an H-representation, an input is redundant if some inequality
can be deleted without changing the polyhedron. It is degenerate
if (in d dimensions) at least one vertex lies on d+1 or more
facets. Similarly in a V-representation an input is
redundant if some input point is not a vertex of the convex
hull. It is degenerate if some facet contains d+1 or more
input points. The options printcobasis and incidence give degeneracy
information. Degeneracy causes pivot or triangulation based
methods such as lrs to run slowly. Redundancy is one
cause of degeneracy, but it can be avoided by pre-processing the
input files. See section redund: extreme Point
Enumeration and Redundant Inequalities for instructions on
how to do this. This pre-processing is unnecessary if it is known
that the input is non-redundant.
Even with redundant input removed a polyhedron may be highly
degenerate. In distribution directory ine/metric there are many
highly degenerate combinatorial polytopes. These are difficult
problems for all vertex enumeration/convex hull programs that
use pivoting, such as lrs. For example, the file cp6.ine
is a polytope with 368 facets in 16 dimensions. It has 32
vertices, but computing these required the evaluation of
4,844,923,002 bases!(see Avis-Jordan, 2017)
Memory considerations
The strong point of lrs is that it
does not save the output produced, so in theory it cannot run
out of memory. With cache size one all memory is allocated
at the beginning, so if lrs starts running it will not
run out of memory. It is possible however that the number of
digits required to do the calculations exceeds the amount
specified on the digits option, or the default. In practice, this
problem will also arise early in the computation. In any case, a
message is printed and the calculation can be restarted. In
order to improve performance, some dictionaries should be
cached. The default of 10 can be overridden by the cacheoption.
If the dictionary is in the cache it does not need to be
recomputed when backtracking, reducing processing time by
about 40%. Since the cache is allocated dynamically, a cache
size that is too large can potentially use up large ammounts of
machine memory.
Geometric Rays
A minimum V-representation of a polyhedron is a minimum set of
vertices and rays such that each point in the polyhedron can be
expressed as a convex combination of vertices plus a non-negative
combination of rays. For the cube, if we delete the inequality
x3 <= 1, i.e.. the line 1 0 0 -1 from file cube.ine,
we get the output:
V-representation
***** 4 rational
1 1 1 -1
0 0 0 1
1 -1 1 -1
1 1 -1 -1
1 -1 -1 -1
end
indicating the polyhedron is the convex combination of 4 vertices
and 1 ray. With the geometric
option, we get the output:
V-representation
begin
***** 4 rational
1 1 1 -1
0 0 0 1 * 1 1 1 -1
1 -1 1 -1
0 0 0 1 * 1 -1 1 -1
1 1 -1 -1
0 0 0 1 * 1 1 -1 -1
1 -1 -1 -1
0 0 0 1 * 1 -1 -1 -1
end
This indicates that geometrically, the polyhedron has 4 parallel
extreme rays (0,0,t) , one incident to each vertex. With the geometric option, all rays will be
printed. Without the option, lrs tries to print each ray
once, but in some cases duplicates will remain, see
subsection Output Duplication.
Output Duplication
For degenerate inputs, pivot based methods for vertex/ray
enumeration such as lrs may generate the same output
ray many times. An output is only printed when it occurs with a
lexicographically minimum basis. This removes all duplicate
vertices, but rays may still be output more than once. This is
due to the fact that duplicate geometric rays cannot always be
detected without storing the output. Since V-representations are
automatically lifted to a higher dimension, this will not happen
for facet enumeration. Unless the allbases
option is specified, lrs makes checks in
order to remove duplicates. A warning message is
produced when duplicates may occur in the output. They can be
removed using the program buffer.c. Two important types
of input never produce duplicate output: polytopes (i.e. bounded
polyhedra) and cones (i.e. polyhedra where the origin is the
only vertex).
Acknowledgements and References
I would like to thank many people for helping with this
implementation project. Komei Fukuda encouraged me from the start,
collaborated in designing the file formats, and provided many
suggestions for improving the code. Debugging would have been
almost impossible without the use of his program cdd as a
benchmark. David Bremner implemented memory allocation, cacheing
and signals. Ambros Marzetta demonstrated the importance of
cacheing and lrslong is based on his earlier implementation of
this as prs_single. Jerry Quinn coded the integer divide
routine. Bug reports were provided by many users, for which I
thank them. In particular Gerardo Garbulsky's extensive use of
earlier versions suggested many refinements and Andreas Enge
helped debug the volume computation. Tallman Nkgau contributed fourier.
D. Avis, lrs: A Revised Implementation of the Reverse Search
Vertex Enumeration Algorithm,
http://cgm.cs.mcgill.ca/~avis/doc/avis/Av98a.ps
In: Polytopes - Combinatorics and Computation, Ed.
G. Kalai and G. Ziegler, Birkhauser-Verlag (2000) 177-198.
D. Avis, "Computational Experience with the Reverse Search
Vertex Enumeration Algorithm," Optimization Methods and
Software, (1998 (to appear)).
http://cgm.cs.mcgill.ca/~avis/doc/avis/Av98b.ps
D. Avis, D. Bremner, and R. Seidel, "How Good are Convex Hull
Algorithms?," Computational Geometry: Theory and Applications,
Vol 7,pp.265-301(1997).
http://cgm.cs.mcgill.ca/~avis/doc/avis/ABS96a.ps
D. Avis and L. Devroye, "Estimating the Number of Vertices of a
Polyhedron," pp. 179-190 in Snapshots of Computational and
Discrete Geometry, ed. D. Avis and P. Bose, School of Computer
Science, McGill University (1994).
http://cgm.cs.mcgill.ca/~avis/doc/avis/AD94a.ps
In: Information Processing Letters, (2000) V. 73, pp.
137-143.
D. Avis and K. Fukuda, "A Pivoting Algorithm for Convex Hulls
and Vertex Enumeration of Arrangements and Polyhedra," Discrete
and Computational Geometry, Vol. 8, pp. 295-313 (1992).
http://cgm.cs.mcgill.ca/~avis/doc/avis/AF92b.ps
D. Avis, K. Fukuda and S. Picozzi, "On Canonical Representations
of Convex Polyhedra", Mathematical Software, ICMS 2002, Ed.
A. Cohen, X-S Gao, N. Takayama, World Scientific, pp.350-360
(2002) http://cgm.cs.mcgill.ca/~avis/doc/avis/AFP02a.ps
D. Avis, G. Rosenberg, R. Savani, B. von Stengel, "Enumeration of Nash Equilibria for
Two-Player Games", Economic
Theory 42(2009) 9-37 pdf
D. Bremner, K. Fukuda and A. Marzetta, Primal-Dual Methods for
Vertex and Facet Enumeration, 13th ACM Symposium on
Computational Geometry SCG 1997, 49-56. http://www.cs.unb.ca/profs/bremner/pd/

