Next: Simple Polygons
Up: Monotonicity Issues
Previous: Polygonal Chains

Recall the convention about the minimum of a polygonal chain introduced earlier,
now we expend it to trees.
Consider intersections constituted of more than 2 edges.
A vertex v is said to be a minimum with respect to a direction d for a
specific intersection if and only if, for every edge leaving this intersection, v is a minimum with respect to d for this edge.
Let EA(v) be the set composed of the edges leaving the vertex v.
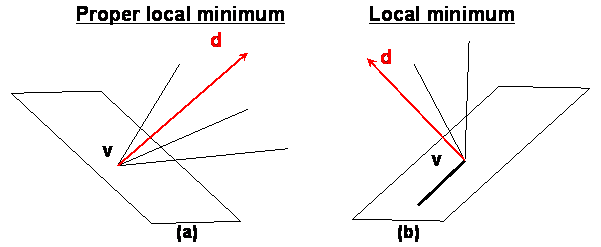
In a tree or a polygon, the vertex v is called a proper local minimum with respect to d.
A local minimum is a vertex with all the edges leaving it included in the half space
defined by {x | vx.d>=0}. Compared to a proper local minimum, an edge passing through a local minimum v could be in the plane perpendicular to d.
The following picture illustrates the difference between the two minimums:
Hence we can give a first result on the monotonicity of a tree:
Now let's discuss the computation of monotonic trees.
If we assume T monotonic with respect to d, it means that r, the root, is the only proper minimum, and no other vertex is a local minimum
with respect to d. By the previous lemma, d cannot be contained in MD(v) for all vertices of T other than the root.
Hence, what do we need to check?
We have to verify if d is contained in MD(v). To say it in another way, we have to check if
for every edge leaving v, v is a minimum with respect to d for EA(v). The only question is:
how many edges leave v? or what is the degree of v in T? Since we have to check every vertex, and the sum of the degree
is linear to the number of vertices, we can compute what we want in O(n) time.
We just find a way of solving our problem with a rooted tree. What if the root is not
specified? We must find it first before checking the monotonicity of the tree.
It could be done easily since the potential root is the only vertex which is supposed to be
a proper local minimum, and d cannot be in the closure of MD(v) for any other vertices of T. This could be verified in linear time.
To answer this question, we need to introduce a new way of representing directions of projections.
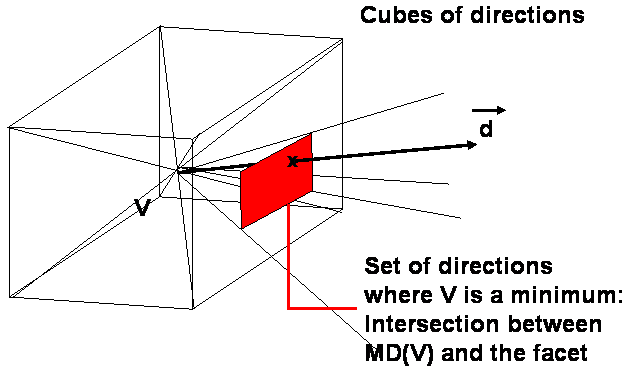
Imagine a cube centered on a vertex v, and each point p on the vertex represents the direction vp.
Let's take any vertex v.
As mentioned earlier, the intersection of MD(v) and the cube represents
the directions for which v is a proper local minimum.
MD(v) intersects the cube with each facet under three different forms:
To understand the demonstration completely, we have to imagine all the vertices and their associated MD(v) concentrated in the center of the cube and imagine all the intersections on the facets of the cube.
Now it is interesting to watch a point on a facet, which represents a direction, and check if
it is inside one or several polygons defined above.
For example, if one point p is in the interior of k polygons, there are k vertices of T that
are local minimum, with respect to Op.
One facet is shown as an example in the next picture:
Now that we know what to look for with such a representation, it seems essential
to know how to compute it.
 Lemma: A rooted tree T is monotonic in direction d if and only of the root r of T is
a proper local minimum and no other vertex is a local minimum with respect to direction d.
Lemma: A rooted tree T is monotonic in direction d if and only of the root r of T is
a proper local minimum and no other vertex is a local minimum with respect to direction d.
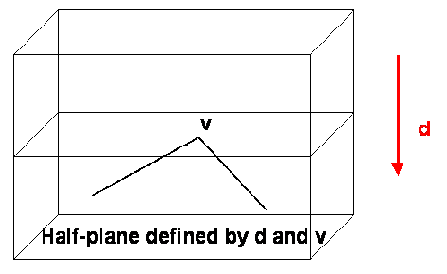
Let MD(v) be the set of directions for which v is a minimum for EA(v). Now consider the half-spaces
delimited by the plan formed by v and its normal d and oriented according to d as shown on the next picture.
 Theorem: Given a rooted tree T, and a direction d, one can decide
in O(n) time if T is monotonic with respect to d.
Theorem: Given an unrooted tree T, and a direction d, one can decide in O(n) time
where n is the number of vertices of T, if there exists a root r of T such that T is monotonic with
respect to d.
Theorem: Given a rooted tree T, and a direction d, one can decide
in O(n) time if T is monotonic with respect to d.
Theorem: Given an unrooted tree T, and a direction d, one can decide in O(n) time
where n is the number of vertices of T, if there exists a root r of T such that T is monotonic with
respect to d.
Given an unrooted tree T, could we find all the roots and directions with respect to which T is monotonic?
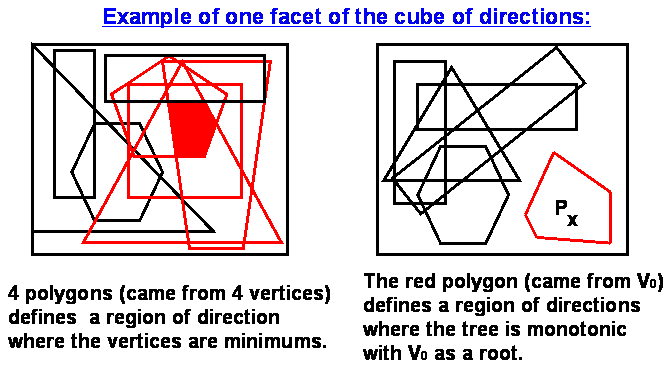
If we find a region on one of the facet of the cube covered by only one polygon,
it means that there is only one vertex v0 defined a set MD(V0)
such that the intersection with the cube of directions is contained in this polygon.
Aha! we got the answer.
This vertex is a root and the intersection defines all the directions of monotonicity
of the tree.
How to compute the set of directions?
For every facet Fi of the cube, we can create the subdivision Ai
composed of all the polygons which are intersections of MD(vi) and the facets.
For every cell of Ai there exists a node and an edge between two nodes if the cells are adjacent.
The graph Gi (planar dual graph of Ai) has O(n2) edges and nodes.
We have to associate every nodes to the number of polygons which are covering it.
Thus starting at any node, we can go to another node through an edge, adding or
subtracting
one to the previous number of polygons and assigning the number to the node.
This procedure can be done in O(n2) time according to the number of nodes and edges in the subdivision. Let's consider the cell covered by only one polygon,
all these cells represent a set of directions and a root from which T is monotonic. The root of T is specified by the vertex generating the convex polygon covering the cell.
Theorem: In O(n2) time, we can determine all directions and roots with respect to which T is monotonic.
![]()
![]()
![]()
Contact us :
Jean HERBIERE and Yueyun SHU