Polygonal Chains

Next: Trees Up: Monotonicity Issues Previous: Monotonicity Issues

Polygonal Chains

Let's start with a polygonal chain P=v₁v₂...v_n, and a direction d.

Observation: A polygonal chain P=v₁v₂...v_n is monotonic in direction d, if the intersection of P with every plane perpendicular to d is empty or a single point.

Is P monotonic in direction $d$ ?

First consider a single segment [ab]. It is monotonic in every direction except those perpendicular to the line segment. Here we are interested in the oriented direction d for whose d.ab>0 (a dot between two vectors denotes dot product, same hereafter).

Let's adopt a new convention:
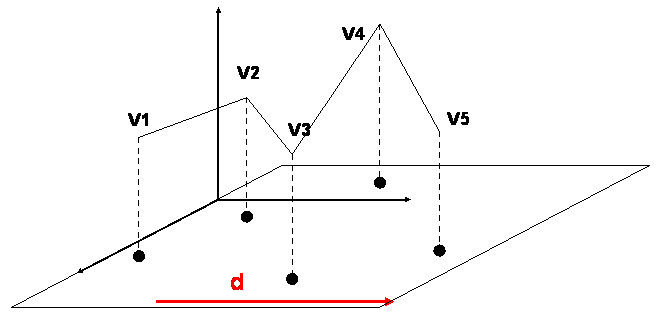
If P is monotonic with respect to d then v₁ (first vertex of P) is a minimum for P with respect to d. For example, if we consider the line segment [ab], a is minimum for all directions d with d.ab>0.

Now consider the whole polygon P, it is monotonic with respect to d if every line segment of P, [v₁ v₂][v₂v₃]... [v_n-1v_n] is monotonic with respect to d. Thus for every i between 1 and n-1, we just need to check every product v_iv_i+1.d>0.

Theorem: Given a polygonal chain P and a direction d, one can determine if P is monotonic with respect to d in O(n) time.

Is P monotonic in some direction?

Let H_i be the half-space determined by {x | Ox.v_iv_i+1>0} (where O is the origin). The set of all directions, for which P is monotonic, is described by the intersection between D and S, where D is the intersection of the H_i over all i, and S is the unit sphere that represents all directions in space (the sphere of directions). Therefore we can tell P's monotonicity by checking if D is non-empty, which could be done in linear time using linear programming.

Theorem: Given a polygonal chain P, one can determine if P is monotonic in O(n) time.

Theorem: Given a polygonal chain P, one can determine in O(nlogn) time all the directions with respect to which P is monotonic.

How to compute all the directions with respect to which P is monotonic?

As noted above, the intersection of D and S describes the set of all the directions from which P is monotonic. The computational complexity is determined by the computing of D (the intersection of the half-spaces H_i). It could be done in O(nlog(n)) time by the following method [3]:

Let's consider the intersection of all the H_i

The intersection is an associative operator, so it is equivalent to write it as

The term in parentheses on the left is an intersection of n/2 half-planes, and hence is a convex polygonal region of at most n/2 sides. The same is true for the term on the right. Since the intersection of two convex polygons can be performed in O(k) time, where k is the side of each the polygon, the previous intersection can be computed in O(n) time. This suggests the following recursive algorithm:

Partition the half-planes in two sets of approximately equal sizes.
Recursively form the intersection of the half-planes in each subproblem.
Merge the subproblems solutions by intersecting the two resulting convex polygonal regions.

If T(n) denotes the time used to form the intersection of n half-planes by this algorithm, we have:

T(n) = 2T(n/2) + O(n) = O(nlog(n)).

Jean HERBIERE and Yueyun SHU