| P |
The set P is the set of the current probe outcomes. |
| Q = (p0, ..., pk) | Q is a sequence of k+1 points that represent the vertices (in clockwise order) of a closed convex region H containing the origin. This set is very similar to the 'inside' region defined previously for our shape from probing algorithms. As we will soon see, the vertices in Q may or may not be contact points resulting from probing. |
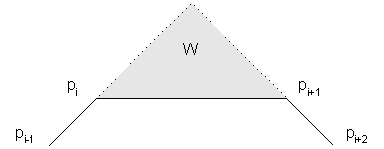
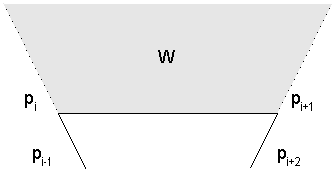
| W[pi,pi+1] | The region W[pi,pi+1] is formed by extending the edges
[pi-1,pi] and [pi+1, pi+2] in the direction of the edge
[pi, pi+1]. The region is either a finite
triangle or an infinite trapeze. These two possibilities are shown in the
following figure. Note that this region W was used extensively in the previous
algorithms to select the best probe (see here).
|
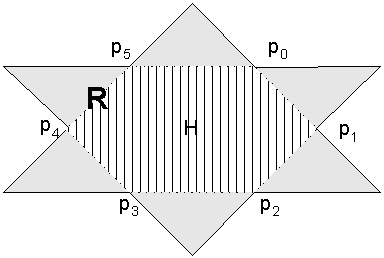
| R |
The region R is the union of the region H (the convex hull of the points in Q) and the regions W[pi, pi+1] of each pair of points in Q. The regions W tend to be finite as the number of points in Q increases so a typical region R has the following shape:
|