Probe Paths Define the Outside Set

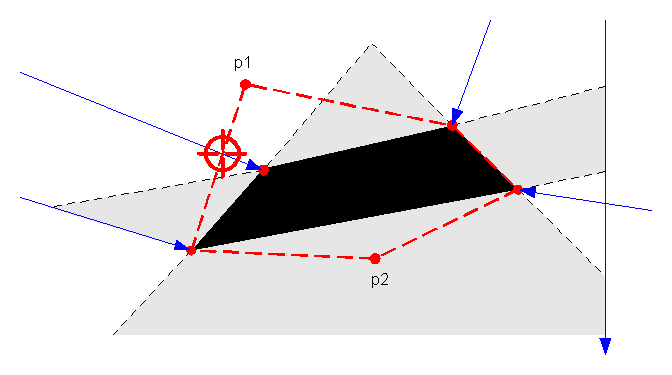
Let's now consider what information can be obtained from the clear path traced by the probe. From the first observation we know that the points lying inside the convex hull of the contact points are inside the shape. Let's now consider each of the points lying outside the convex hull. Consider, for example, the point p1 shown in the diagram below. If p1 is part of the shape than the convex hull has to be extended to include it. Observe however that extending the convex hull causes a conflict with one of the probe outcomes. The crosshair shows that a contact should have occurred on the new convex hull, thus preventing the probe from reaching one of the known contact points. This contradiction implies that p1 is not part of the shape. This points is thus move from the maybe set to the outside set.

Let's now consider the point p2. As can be seen in the diagram, the convex hull can be extended to include it without contradicting the known probe outcomes. Thus p2 is a candidate for inclusion in the shape. It may or may not be part of the shape: we do not have enough information to decide. It remains in the maybe set.

This procedure can be repeated for all the points in the maybe set. Some points will remain in the maybe set while others will be moved to the outside set. Note that the decision is final: a point that is moved to the outside or inside set is never moved back into the maybe set.

The above discussion used intuitive arguments to show that some points can be rejected based on the probe outcomes. We will now describe a more formal mathematical or geometrical argument. Consider a point in the maybe set. This point is moved to the outside set if and only if there exists a line joining it to a point of the inside set such that this line intercepts a probe before it touched the known contact point. For example, p1 has to be moved to the outside set because the line joining it to the bottom-left contact point intercepts the probe. The point p2, on the other hand, remains in the maybe set because no line between it and the inside set that intercepts a probe exists .

These assertions will now be proved. By definition, a convex polygon is such that lines joining any two of its vertices must be entirely within the polygon. If this properties holds then it follows that lines joining any two points within the bound of the polygon must also fall within the polygon. Let's now consider points in the maybe set for inclusion in the inside set. In order for one of these points to be a candidate, any line joining it with a point of the inside set must also fall entirely inside the polygon. Since the bounds of the polygon are not known yet, this property cannot be used to confirm that points belong to the shape. It can, however, be used to show that points in the maybe set cannot be part of the shape and thus belong in the outside set. As explained before, points on the path of the probe cannot be part of the shape. Thus if a line joining a point in the maybe set and a point in the inside set intersects a probe path, this implies that the line is not inside the shape and neither is the point of the maybe set. The point can then moved to the outside set.

Contact Points Define the Inside Set

Colinear Contact Points Define Edges or Edge Segments