Applet Implementation Details
This page describes at a high level how the hyperplane construction algorithm
was implemented in the Java applet. In
order for this to make sense, you should review the process of hyperplane
construction.
Goal of Hyperplane Construction
Recall that the goal in hyperplane construction is given a set of Tomek
links, find out if there is a hyperplane that:
-
Cuts all Tomek links such that prototypes
on one side belong to a single class
-
Classifies all data points associated with prototypes below a maximum acceptable
error threshold.
These steps are implemented the same order, and are described below.
Step 1: Cutting All Tomek links such that Prototypes
on One Side Belong to a Single Class
The first step in the implementation is to determine if a hyperplane exists
that cuts all Tomek links, while ensuring that all prototypes one side
of the hyperplane belong to a single class (refered to as the class
limitation in the algorithm description). This step is implemented
by drawing lines between all prototypes belonging to different Tomek links,
and checking if:
-
For each Tomek link, one prototype falls on each side of the line
-
All prototypes on one side belong to a single class
-
All prototypes on the other side belong to different classes
If a line exists that passes these three checks, we know there exists a
hyperplane that cuts all Tomek links and satisties the class limitation.
Figures 1 and 2 below show the examples of check success and a failure,
respectively. The purple line representes the testing line.
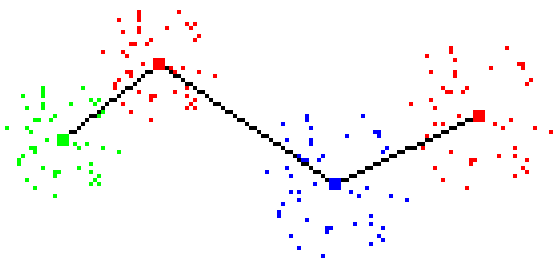

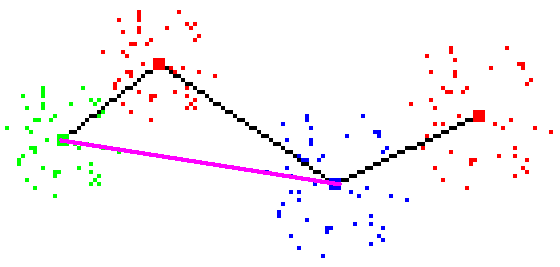
Figure 1 - Check success: line cuts all Tomek links and prototypes above
line are always red
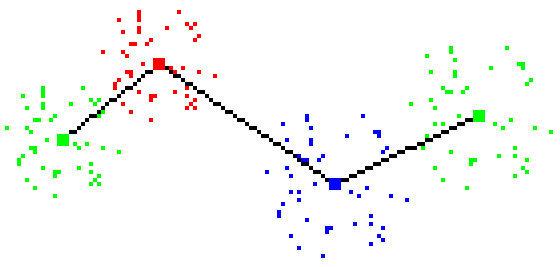

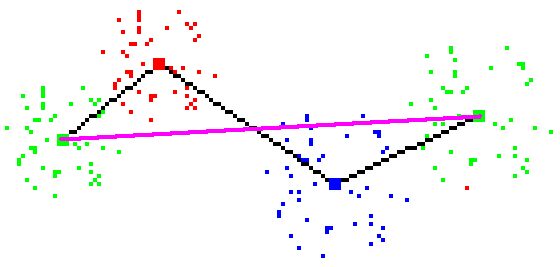
Figure 2 - Check failure: line cuts all Tomek links, but class limitation
is never satisfied
Step 2: Classifying Data Points Associated with Prototypes
Below a Maximum Acceptable Error threshold
After it has been verified that a hyperplane exists which cuts all Tomek
links while maintaining the class limitation, the second step is to verify
that a hyperplane exists which classifies all related data points below
a maximum acceptable error threshold. This is done in a brute force way:
drawing lines between all data points, and for each line:
-
Verifying that the line cuts all Tomek links
-
Classifying all data points, and determining whether the error is less
that the maximum error threshold
Verifying that the line cuts all Tomek links is implemented in much the
same way as step 1 described above. The only difference is that the class
limitation is not longer considered. Since it has already been verified
that a line exists which cuts all Tomek links according to the class limitation,
every
line that cuts all Tomek links must also do so.
Once a line has been found to cut all Tomek links, classification is
performed on all data points. At this point, it is know that all prototypes
on one side of the line are of a single class, and all prototypes on the
other side are of different classes. The classification is therefore binary.
Lines are tested until one is found that classifies all data points with
an error rate less that the maximum error threshold. If line is found,
there exists no hyperplane that fulfills our goal. If a line is found,
it is kept as the hyperplane corresponding to the set of Tomek links.
Figures 3, 4 and 5 below illustrate two check failure cases and one
success.
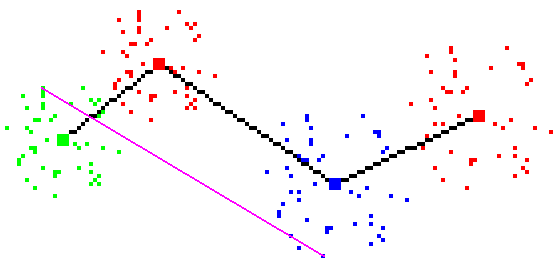
Figure 3 - Check failure: line does not cut all Tomek Links
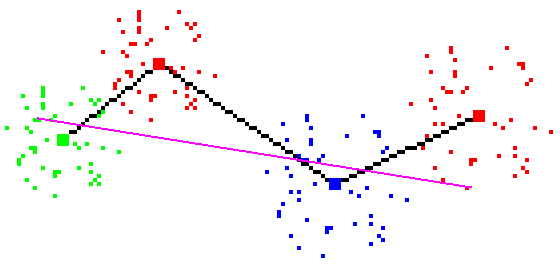
Figure 4 - Check failure: line classifies data points with high error
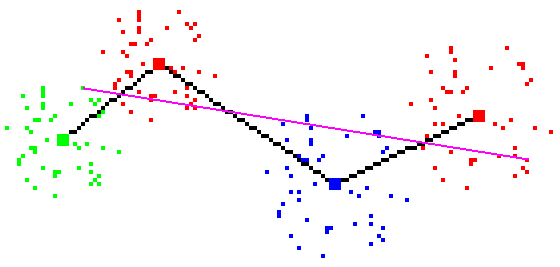
Figure 5 - Check success: line classifies data points with acceptable error
A Word on Complexity
The implementation of the algorithm quite complex. Step 1 is O(N2)
in the number of prototypes in the worst case, but this is not significant
because the number of prototypes is typically small. Step 2 is O(N3)
in the number of data points in the worst case: the product of O(N2)
to generate all possible lines between data points and O(N) for the classification
stage. This is significant because there are typically lot of data points.
By using clever tricks this complexity can be reduced. From the geometry
of the Tomek links, it can be seen that a significant number of data points
can never be part of a line that will cut all Tomek links (see figure 6).
These can be completely removed from the O(N2) line generation
stage. This is illustrated in Figure 6 below.
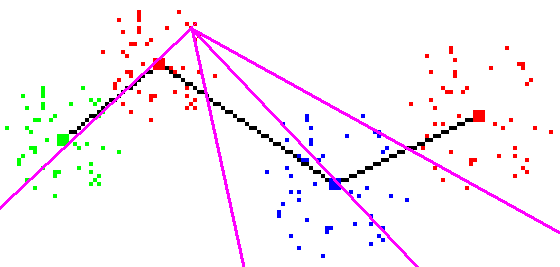
Figure 6 - Lines from some data points will never cut all Tomek links.
Also, when performing the classification on a test line, classification
need not proceed if it has been determined that the error rate is already
too high. Prematurely terminating the classification stage reduces the
complexity of the O(N) classification stage.
This web page prepared by
Matt Toews (mtoews@cim.mcgill.ca)
as a term project for the course
Computer
Science 644 - Pattern Recognition
at the
McGill Center for
Intelligent Machines



![]()






