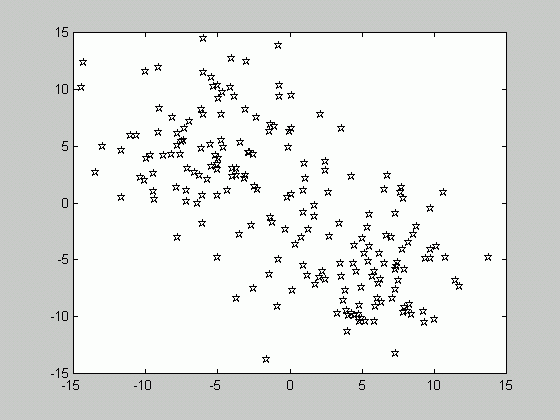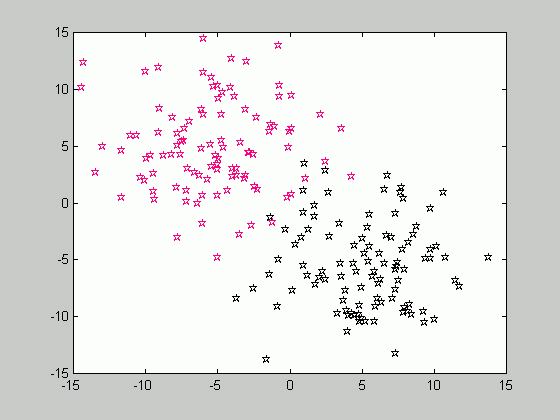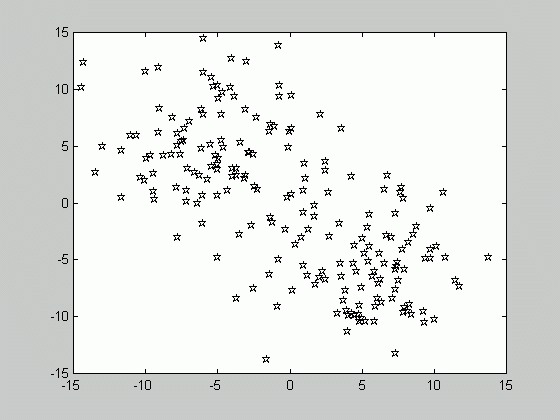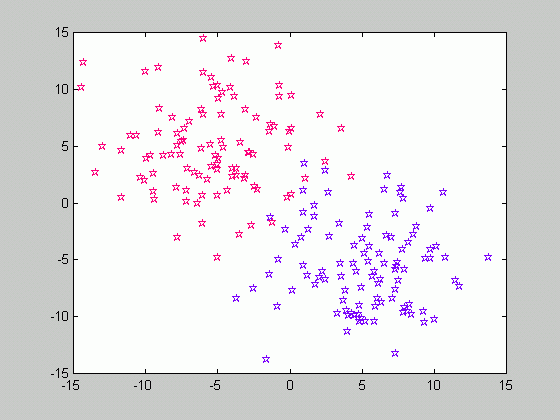
Let's recall that in order to compute the a posteriori probability P(w|x), the class-conditional densities p(x|w) are to be estimated for each class. Suppose that in order to perform estimation, we are given a set of samples X consisting of the subsets X₁, X₂, ..,X_c, where c is the number of classes and the samples of X_k belong to class w_k. Consider the class-conditional density function of a class w_k given the set of samples p(x|w_k, X ). It is quite obvious that only the samples drawn from the same class, i.e. the subset X_k may influence the value of the above-mentioned probability. Therefore, p(x|w_k, X )=p(x|w_k, X_k ).

Furthermore,  we can now reduce the class notation because all the samples used in the formula are drawn from the same class. In other words, we have just reduced our problem of estimating the class-conditional densities to the problem of estimating an unknown density function p(x) from which the set of samples X is drawn.

In the figure above, the samples are drawn from two classes, w₁ and w₂. We are dealing with the supervised case, that is the state of nature (class label) for each sample is known. Therefore, we can divide the set of samples according to the class they belong to, and solve the problem of estimating the class-conditional densities separately for each class.

Currently our problem is reduced to computing the estimate p(x|X) of the probability density function p(x).

As we already mentioned in the introduction section, the approach presented here assumes that the form of the probability density p(x) is known while the distribution parameters are those needed to be estimated. In other words, given a vector of parameters , the function p(x|) is completely known. In case of normal distribution is composed of the mean vector and the covariance matrix elements. Another assumption we make is that the a priori distribution of the parameters p( ) is known.

Let's now see how p(x|X) can be computed.

As was mentioned above, the density function p(x| ) is known. In order to find p( | X) we can apply Bayes rule.

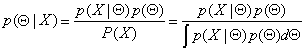
We stated earlier that the distribution of parameters p( ) is known. If we make another assumption that the samples are drawn independently, then the p( X|) term can be decomposed as follows:

Using the formulas above, the cross-conditional density functions p(x|w_k) can be obtained for every class w_k. In the sections that follow we'll take a detailed look at the case where these density functions are assumed to have normal distribution. Below we'll look at a simple though impractical example illustrating the formulas.

Suppose we have two coins. They look the same, but we know that one of them is fair (P(head)=0.5) while the second is not (P(head)=0.3). A coin is picked randomly (with probability 0.5 ) and tossed 100 times. 40 heads occurred. What is the probability of obtaining a head if the picked coin is tossed?

Let's now try to formulate the problem in terms of the notations we developed earlier.

Obviously, the only parameter here is the probability of obtaining head.

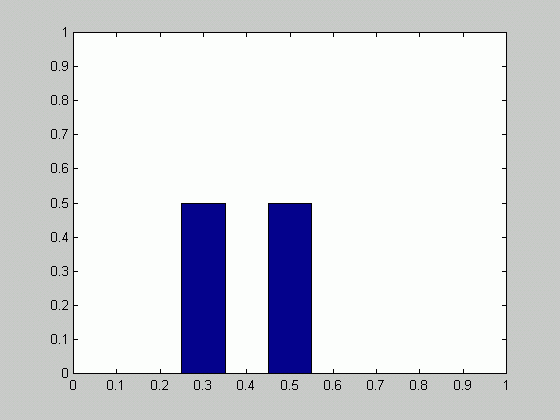
X is the set of samples. Let's assume that the order of the samples is known as well as the number of heads. For instance,

Therefore, it holds that

Then,

From the formulas above p( | X ) can be easily obtained:

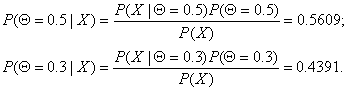
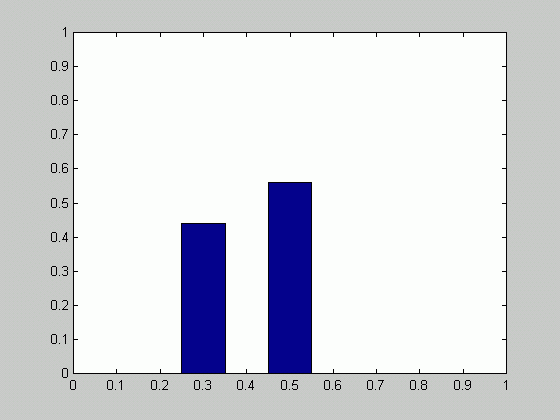
Finally,

which answers the question of what is the probability of obtaining head given the samples.

Click here to play with an applet demonstrating the example above.