Definitions
Definitions
Some Musical Terms
We begin this section by defining some musical terms that will be used throughout this tutorial.
Polyphony – Polyphonic music is music that uses many independent voices simultaneously. The word comes from the greek for “many sounds”. Most of the music we hear today is polyphonic, except for some (typically folk or children's) songs for unaccompanied voice.
Pitch – The pitch of a note is the perceived frequency of that note. A common intuitive description of the pitch of a note is how “high” or “low” it sounds. Interested readers can also consult this Wikipedia article for a thorough examination of the definition of pitch and historical pitch standards in western music.
Music Notation
There are many ways to represent the same musical piece. For musicians, the most familiar notation system is probably the standard western music notation system:

Figure
1 – Standard musical score representation of J.S. Bach's
Invention 1
However, for computational purposes it is convenient to represent musical piece in other ways. For instance, we can represent the above fragment of music as a string of characters:
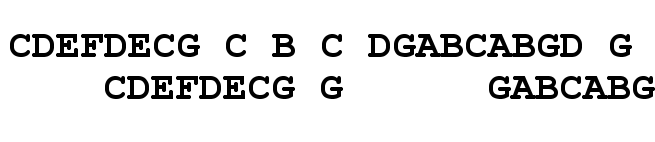
Figure
2 – String representation of J.S. Bach's Invention 1
This representation has the advantage of allowing fast text searches on the data, using standard computational string matching techniques. However, a string representation does not lend itself very well to the representation of polyphonic music.
Geometric representations can be more effective in expressing polyphonic music. An especially natural geometric representation of music is the horizontal line segment representation. In this format, musical notes are represented by horizontal lines in the plane. The pitch of the note is represented by the vertical position of the note, while its location in time within the piece is represented by the horizontal position and length of the line segment. Here is the line segment representation of the above musical fragment:
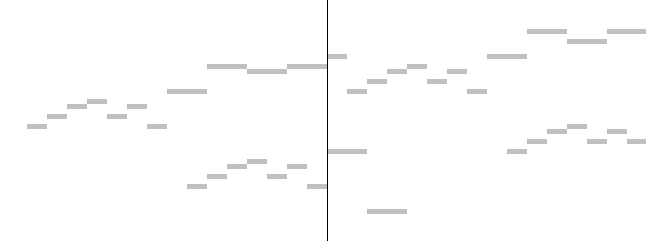
Figure
3: Line segment representation of J.S. Bach's Invention 1
This representation has many advantages. On top of being able to naturally represent polyphonic music, it also can be searched efficiently. Furthermore, it is also a flexible representation that enables search methods to use various distance metrics. For these reasons, this is the representation that is used in Lubiw's and Taner's algorithm for music pattern matching.
Calculating the Similarity of Individual Notes
Underlying any pattern matching algorithm for musical sequences is an underlying concept of the “similarity” between any two notes. Many note attributes could be used to differentiate two notes: their pitch, tone, loudness, duration, relation to nearby notes, could all be used to determine which notes are similar, and which ones are not. For this tutorial, we will only consider one of those attributes: the pitch of the notes.
Given the pitch of two notes, we can then determine the distance between the two notes by using a weight table for all possible intervals. Three such possible tables are outlined below:
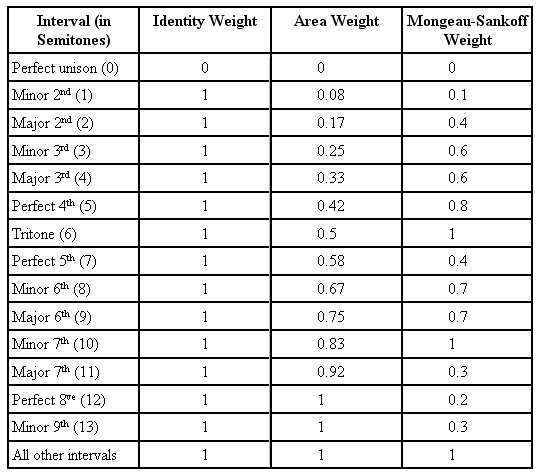
Table
1: Three weight functions for all possible intervals
The simplest distance weight function is the identity function. For this distance function, two notes with the same pitch are identical, and thus have a distance weight of zero. However, all notes with different pitch values are considered equally different from each other, so they all have a distance value of 1. This distance function is appropriate for finding exact matches of a pattern within a score, but does not perform very well for approximate pattern matching.
A better distance weight function for approximate pattern matching was examined by Aloupis et al. in their paper entitled Computing the similarity of two melodies. In this paper, the distance weight of two notes corresponds to measuring the area between the line segments for the two notes in the horizontal line segment representation. Therefore, the distance weight at a specific point between two notes is directly proportional to the distance between the two notes' pitches. This measure better represents the heuristic that notes that have closer pitch usually do not sound as “far away” from each other as notes separated by very large intervals.
However, that distance function is still not ideal because the pitch distance heuristic does not take relative dissonance of intervals into account. Notes separated by consonant intervals such as the octave usually sound “closer” than notes separated by highly dissonant intervals such as the tritone (also known as the augmented fourth or diminished fifth). In order to capture the effect of dissonance on the perceived distance between notes, we can use a custom distance weight function such as the one that was presented by Mongeau and Sankoff in 1990. Generally, this distance function will return more perceptually relevant approximate pattern matches than either the identity or area weight functions.
~ ~ ~ ~ ~ ~
Next Page: Algorithm