Algorithm

The problem

The problem of finding the occurrences of a musical pattern within a larger musical score can be stated more formally as follows: given the following input,

A musical pattern of m notes
A score of n notes (with n > m)
A weight function f that measures the similarity between two notes
A minimum match threshold

a music pattern matching algorithm should find all translations of the musical pattern in time and pitch where the pattern and the score have a match score higher than the minimum match threshold.

Overview of the algorithm

The Lubiw and Tanur algorithm for solving the music pattern matching problem uses the horizontal line segment geometric representation of the pattern and the score. In order to visualize the algorithm's process, we can imagine the score being written on a piece of paper, and the pattern being written on a separate piece of transparency. The algorithm then proceeds to place the pattern on top of the score. As we have seen in the definitions page, for this problem we are not concerned with the absolute pitch of the pattern, so the algorithm will test the pattern with all possible pitch transpositions. Each pitch transposition corresponds to a vertical translation of the pattern with respect to the score. In order to find all occurrences of the pattern throughout the score, the algorithm will also test the pattern against all possible translations in time. This corresponds to horizontal translations of the pattern with respect to the score.

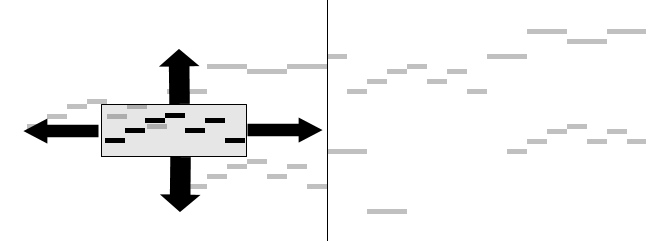
Figure 1: Sweeping the pattern horizontally and vertically over the score

With all these horizontal and vertical translations, the algorithm will have effectively completed a sweep of the pattern over the musical score. As such, it will have calculated the match score for every candidate translation and retained all the translations that have a score above the minimum match threshold. All these translations will correspond to occurrences of the pattern in the score.

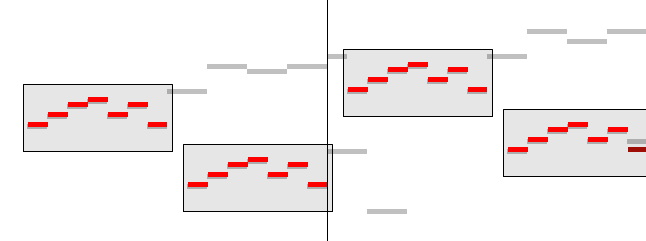
Figure 2: Three exact and one approximate matches retained after the pattern sweep

Calculating the match score of a translation

For each candidate translation, the match quality is measured using one of the weight functions covered in the Definitions page. The weight function calculates the distance between pattern and score notes at all points. The total weight of the match is then defined to be the sum of all distance weights times their length in time. This is best shown graphically with an example:

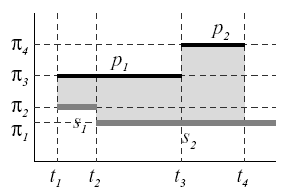
Figure 3: Weighted Distance Between the notes of p and s

In this above case, the weighted distance between the pattern p and the score s is:

where is the weight function between two notes.

Complexity Analysis

It is possible to design an O(nmd log m) algorithm that implements the above heuristics, where n is the number of notes in the score, m is the number of notes in the pattern, and d is the number of possible pitches for the notes. To show how this is done, we first proceed to establish upper bounds on the minimum number of candidate translations of the pattern that we need to examine in order to find all the best possible matches. We then describe optimization methods that enable each candidate translation to be tested in constant time, giving the desired complexity.

Establishing Upper Bounds on the Minimum Number of Translations

Let's begin by establishing an upper bound in the number of pitch translations for our pattern. This one is straightforward: we assume that there is only a finite number of possible pitches for each note. Let that number of possible pitches be defined as d. Then we can translate the pattern so that its first note begins at each of these possible pitches. This gives us a total of d possible pitch translations for the pattern at any given time point.

Establishing an upper bound on the minimum number of pattern translations in time is slightly more complicated. In order to do this, we can use the following claim:

Claim 1: The optimal pattern matches onto the score occur when the start or the end of a note in the pattern coincides with the start or the end of a note in the score.

To prove this claim, it is only necessary to show that when we translate a pattern by some small where the start and end of the pattern notes do not cross the beginning or the end of a note in the score, then the match score of the pattern on the score does not change. The technical proof of this fact will not be included in this document, but it can be demonstrated visually as follows:

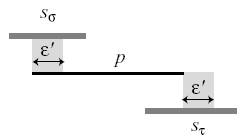
Figure 4: Shifting the pattern by

We now have an upper bound of nm possible translations of the pattern in time over the score, because the claim above guarantees that there can be at most nm possible candidate translations for the optimal pattern matches. Therefore, in total we have nmd candidate translations of the pattern over the score.

Searching all Candidate Translations Efficiently

The most efficient traversal of all the candidate translations proceeds by fixing the pattern at a single pitch translation, and then iteratively testing all the time translations at that pitch. Finding the pitch translations takes constant time, since we are simply trying all different pitch translations. However, finding the next time translation is a little more complicated: to find the next candidate translation, we need to find the next point in time in which the start or end of a pattern note coincides with the start or end of a note in the score. This can be done in O(log m) time by using a heap of the next time point of interest for each note in the pattern. With this heap, we can traverse all candidate translations in O(nmd log m) time.

Recomputing the match score of a translation from scratch for each candidate translations of the pattern on the score would take at least O(m) time. However, it is not necessary to do that. As a result of the Claim 1 above, we can update the score of a translation of the pattern in constant time by using the score of the previous candidate translation in time. The details of this method is beyond the scope of this tutorial, but is described in detail in the article by Lubiw & Tanur. This constant time update results in a total time complexity of O(nmd log m) for the algorithm.

~ ~ ~ ~ ~

Next Page: Examples