
Consider an embedding of a planar graph. A face of the graph is a region bounded by a set of edges and vertices in the embedding. Note that in any embedding of a graph in the plane, the faces are the same in terms of the graph, though they may be different regions in the plane. The face with unbounded area is known as the unbounded face, the outer face, or the infinite face.
Relating the number of faces (F), edges (F), vertices (V), and components (C) in a planar graph, Euler's formula states that V-E+F=C+1. Noting that every edge borders exactly two faces, we can be assured that the number of edges in a planar graph is linear in the number of vertices.
These graphs are planar:
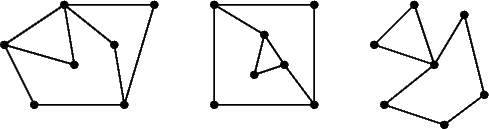
But these graphs are not:
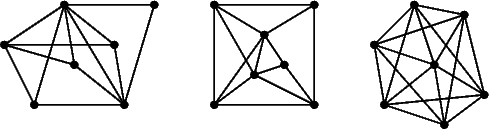
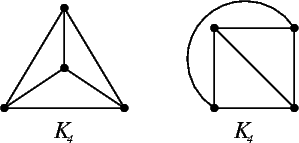
Planar graphs are all well and good, but we wish to consider the problem of straight-line embeddings in a given point set. Consider, for example, K4 in the two point sets shown. Although K4 is planar, it cannot be embedded in the second point set if we demand that the edges be straight lines. What, then, is the largest class of graphs that can be straight-line embedded in any point set? Gritzmann et al. showed that it is exactly the class of outer-planar graphs [GMPP91]. Castañeda and Urrutia showed the same independently in 1996 [CU96].
These graphs are outer-planar:
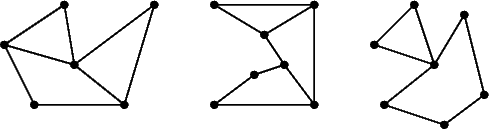
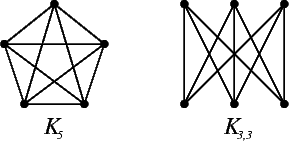
But these graphs are not (although they are all planar):
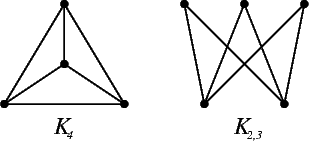
Just as planar graphs have a graph minor characterization as seen in Kuratowski's theorem, a beautiful analogue can be found for outer-planar graphs: A graph is outer-planar if and only if it contains neither K4 nor K2,3 as a minor.