Embedding an outer-planar graph in a point set

Connectivity reductions:

A graph is connected if there is a path in the graph between any two vertices. It is k-connected if it remains connected if any k vertices are removed. Bose et al. [BMS95] showed that any algorithm for embedding an outer-planar graph in a point set has time complexity at least O(n log n). What we want to do now is show that if the graph is disconnected or has a cutvertex (i.e. is not 2-connected) then we can efficiently subdivide the problem of embedding the graph into two or more smaller sub-problems.

If the graph is disconnected, we can sort the point set by angle with some outside point (that is not in the point set), partition the point set appropriately, and embed the graph's connected components in the partitions of the point set.
If the graph is connected but has a cutvertex v, we can sort the point set by angle with some point p, partition the point set (excluding an extreme point p) appropriately, and embed the cut components of in the partitions, joining them at p.

Both of these reductions can be done in O(n log n) time, so they will not change the time complexity of the algorithm, since it must take at least O(n log n) time already.

Let's consider one final reduction. Suppose we can embed maximal outer-planar graphs efficiently (that is, no edges can be added inside to the graph if it is to remain outer-planar). Then given any outer-planar graph, we can add edges to it until it is maximal, embed the resulting maximal graph, then remove all added edges from the embedding. Again, this modification can be done in O(n log n) time, so we need only concern ourselves with maximal graphs.

The difficult part, then, is embedding maximal 2-connected outer-planar graphs efficiently. To do this, we will use something called an (r,s)-triangle, the key to finding our embeddings. From here on in, we will assume our outer-planar graphs are maximal and 2-connected.

Note that in a maximal outer-planar graph, each bounded face is a triangle. Note also that in a 2-connected outer-planar graph, the unbounded face is a cycle since it contains no cutvertices. This means that a straight-line embedding of a maximal outer-planar graph is equivalent to a triangulation of a polygon on the point set.

Defining (r,s)-triangles:

The notion of an (r,s)-triangle exists for both maximal outer-planar graphs and point sets.

In an outer-planar graph (remember, each bounded face is a triangle since we assume the graph is maximal), an (r,s)-triangle is a face in the graph with at least one edge on the unbounded face such that deleting the vertices of the triangle cuts the graph into two outer-planar graphs of size r and s. Note that r and s must be non-negative, and r+s = n-3.

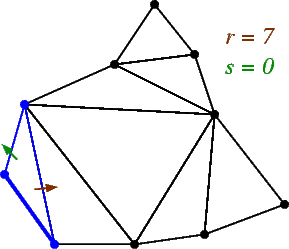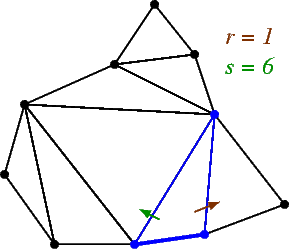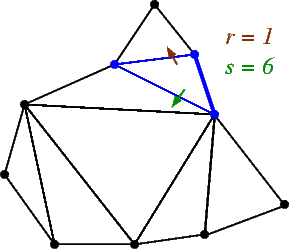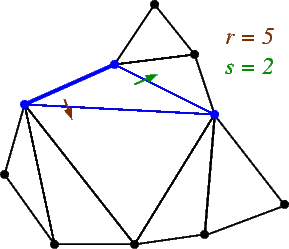
In this example, every triangle with an edge on the outer face is shown, along with its corresponding values of r and s.

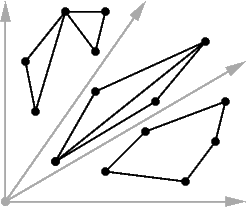
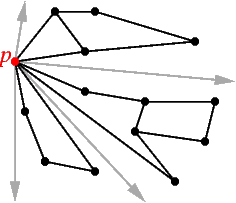
In a point set, an (r,s)-triangle is a triangle Δabc such that the following hold:

a and b both lie on the point set's convex hull.
The interior of Δabc contains no other point in the point.
There is a line that passes through both c and the line ab such that excluding a, b, and c, r points are on the "right" side of the line and s points are on the other side of the line.

Note that again, r and s must be non-negative and their sum must be n-3.

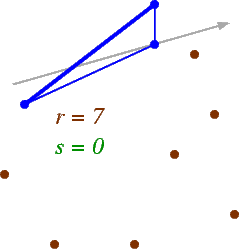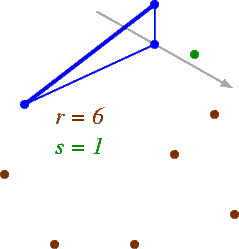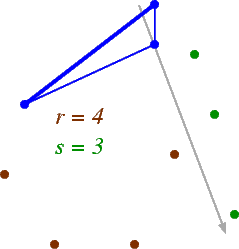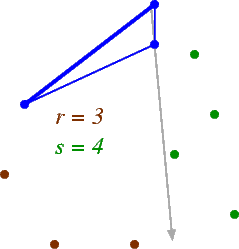
In this example, the triangle shown is a (7,0)-triangle, a (6,1)-triangle, a (5,2)-triangle, a (4,3)-triangle, and a (3,4)-triangle. Unlike (r,s)-triangles in graphs, a single triangle in a point set can be an (r,s)-triangle for several different values of r and s.