Embedding an outer-planar graph in a point set

Finding (r,s)-triangles:

The following theorem is the key to the embedding algorithm:

Theorem: Given two vertices a and b that are consecutive in the convex hull of a point set of size n, along with non-negative r and s such that r+s = n-3, there is a point c in the set such that Δabc is an (r,s)-triangle.

The proof of this theorem, given by Bose, shows us how to construct these triangles [B02]:

Find a line l through a such that exactly r+1 points are on the "right" side of l.
Of these r+1 points, let c be the point that is hit first when rotating a line clockwise about b from a.

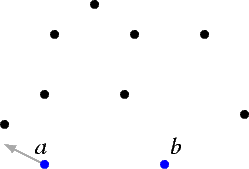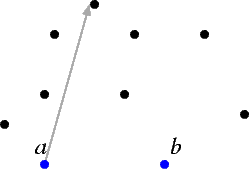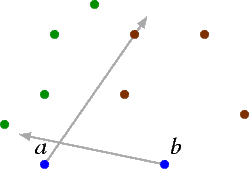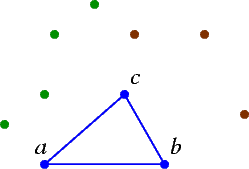
It is fairly evident why this will produce the desired (r,s)-triangle. We also know from this what our "r" points are and what our "s" points are. We say that the "r" points lie to the right of the (r,s)-triangle and the "s" points lie to the left of the triangle. In the example illustratred, we are looking for a (3,5)-triangle.

To find an (r,s)-triangle, no sorting of the point sets needs to be done. In fact, finding the triangle can be done in O(n) time using linear selection and well-known geometric methods [CLR90, B02].

The embedding algorithm:

It is finally time to describe the recursive embedding algorithm. This algorithm embeds 2-connected maximal outer-planar graphs; refer to the section on connectivity for the reasoning behind this. Go to the applet section and try it out!

Embed(G, P, u, v, a, b):

Input: A graph G on n vertices, a set P of n points in the plane, a special edge uv on the outer face of the graph, and two special points a and b that are consecutive on the convex hull.

Output: An embedding of the graph in the point set.

If n < 3 then we are done.

Since G is maximal and u and v are on the outer face, u and v share a unique neighbour w. Δuvw is an (r,s)-triangle for some r and s. Find r and s.

Now that we have r and s, find the point c in P such that Δabc is an (r,s)-triangle. Put edges between a, b, and c. That is, "embed" the (r,s)-triangle from the graph into the (r,s)-triangle from the point set.

Let G₁ be the subgraph of G induced by v, w, and the r vertices to the right of Δuvw. Let P₁ be the subset of P consisting of b, c, and the r points to the right of Δabc. Call Embed(G₁, P₁, w, v, c, b).

Let G₂ be the subgraph of G induced by u, w, and the s vertices to the left of Δuvw. Let P₂ be the subset of P consisting of a, c, and the s points to the left of Δabc. Call Embed(G₂, P₂, u, w, a, c).

The initial values of u, v, a, and c can be chosen using whatever you like. Here we see an example of how to split the graph and the point set.

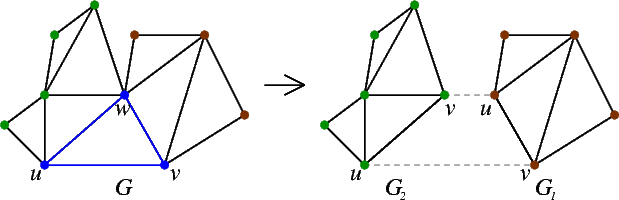
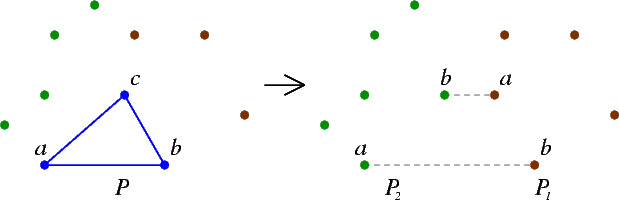
We can see that our recursion tree is, in fact, the dual of the graph G. Each time we are at a node in the recursion tree, we are embedding the corresponding face of the graph (which is a triangle), then moving to the neighbouring faces that we have not yet visited.

We would, of course, like to know the complexity of the algorithm. Finding r and s, embedding the face, and splitting up the graph and the point set can all be done in O(n) time. As mentioned earlier, so can finding the (r,s)-triangle in the point set. This means that the time complexity of the entire algorithm is O(nd), where d is the depth of the recursion tree. Of course, d is at most the diameter of G*. The best value possible for d is O(log n), and the worst possible value is O(n). Hence the algorithm's running time, in the worst case, is O(n²).

Bose devised a similar, more efficient algorithm that runs in O(n log³n) time, but it relies on complex data structures [B02]. It is not currently known whether or not an O(n log n) algorithm exists.