Next: Applet Up: Previous: Projection with distinct x-coordinates Contents
Definition: A camera such that the image does not contain any parallel lines.
More precisely, considering every line Li built from two points
Ai = (xAi, yAi, zAi) and
Bi = (xBi, yBi, zBi), we would like no two projected line li parallel to lj
(j ![]() i).
i).
If such event occurs, then it is impossible to define a valid projection because both line will be parallel for any projection center. So the first step of the algorithm would be to detect if it is the case. This can be done in O(n log n) with this procedure:
For every line Li = Ai, Bi assume that the Rt transformation have been applied. This simplifies the rest of the algorithm because the projection plane is now at Z = 1. Check for points parallel to the projection plane with zAi = zBi. Each line in that set is intersected with the unit half-circle with positive x-coordinates and the intersection points are kept (figure 10:
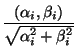
where
and
Two lines li, lj are parallel if
![]() =
= ![]() . Since the unit half-circle with positive x-coordinates is monotonic in Y, then we can sort w.r.t Y values of the intersections and check for duplicates. This can be achieved
O(n log n).
. Since the unit half-circle with positive x-coordinates is monotonic in Y, then we can sort w.r.t Y values of the intersections and check for duplicates. This can be achieved
O(n log n).
To check this condition, we use an algorithm very similar to the one described in the previous section. We can define each line of the projection in the same way as previously, except that each line is defined with 2-D points. The only difference is that each line needs to be considered by computing the Il value. Again by sorting, we can check if two lines are parallel in the image plane in O(n log n).
Here is a summary of the algorithm:
![\framebox[6.0in]{
\begin{minipage}[h]{5.0in}
\par
for each line $l_i$\par
~~~~i...
...\textcolor{Red}{$O(n~log~n)$}\\
\par
Check for duplicates
\par
\end{minipage} }](img28.png)
Every pair of segments defines forbidden projection centers. This happens when the slope of the two projected Line li and lj are equal:
Like before, let's apply the transformation RT to each point in space so that the projection plane is Z = 1 and the projection center c is located somewhere on the Z-axis with cz < = 0 and cx = cy = 0. In this particular configuration, the projection of each point on the projection plane has the form:
where (x, y, z) is the point in space. Notice that the focal length is not in the equation. This is simply because the distance to the plane is not important, only the relative distance of the projection center and the object changes the parallelism of the lines. We can use this relation for the points defining the two lines in the slopes inequalities. Rearranging the equation yields this relation:
which is of the form (thanks to Mathematica) :
| Acz2 + Bcz + C = 0 |
where,
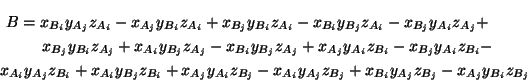
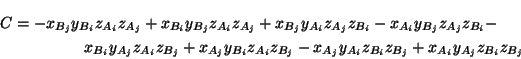
which is a polynomial of degree two in cz. Thus, solving this inequality yield at most two forbidden projection center on the Z-axis. Therefore, the Z-axis is not a line of forbidden projection center (more generally, the projection axis) and that conclude the proof. A very similar proof is presented in [1].
Again, we present a slightly modified algorithm from the one presented in [1]. Let's assume a set of lines Li and the projection J0 with projection center c0. Again, let's also assume that c0 is located at the origin and all points Pi are in front of the projection plane at Z = 1 and have positive coordinates.
Project each Li using J0. With the algorithm presented before, check if no two line li are parallel. If so, c0 is a valid projection center. Otherwise, let's define c1 the closest forbidden projection center such that
c1, z < c0, z (getting further away from the Li). Then there are at least two points Lij and
Lij + 1 whose projections are parallel. Moving the projection center from c0 to c1 is a continuous transformation, showing that the line Lij and
Lij + 1 were already consecutive in their ![]() value. Therefore, we only need to consider each pair of consecutive line in the sorted list of
value. Therefore, we only need to consider each pair of consecutive line in the sorted list of ![]() as possible pairs of points defining c1. To find c1, we consider each one of those pair of line and solve the polynomial equation shown before. This is done in O(n). Then, we choose c1 as the closest intersection to c0. Any point on the open line segment
as possible pairs of points defining c1. To find c1, we consider each one of those pair of line and solve the polynomial equation shown before. This is done in O(n). Then, we choose c1 as the closest intersection to c0. Any point on the open line segment
![]() is allowed.
is allowed.
Here is a summary:
![\framebox[6.0in]{
\begin{minipage}[h]{5.0in}
\par
Project each $L_i$\ from $c_0...
...Any point on the open line $\overline{c_0c_1}$\ is allowed
\par
\end{minipage} }](img42.png)
Greg ALOUPIS 2003-12-22