Computing shortes transversal

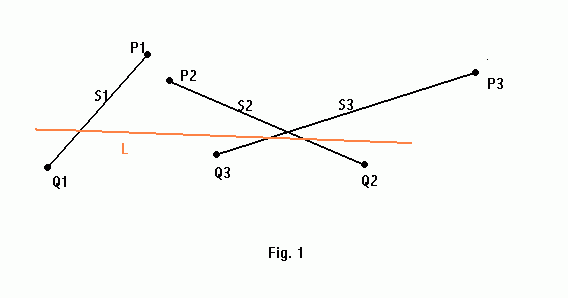
We already know how to find a stabbing line, or a transversal of a line segments set. In this section we'll learn how to compute the shortest such transversal. Note that this topic is rather complicated and could be a subject to a project all by itself. Therefore, here only a simplified version is presented.

Let S = { S1, S2, ..., Sn} be a set of line segments and L be its stabbing line (transversal). We'll assume L is not vertical.

Let a(Si , L) denote the end point of Si which lies above L, and b(Si, L) -- end point which lies below L.

In figure 1, a(S1, L) = P1; b(S2, L) = Q2.

Also, let A(S, L) = { a(S1, L), a(S2, L), ... a(Sn, L) }, and similarly B(S, L) = { b(S1, L), b(S2, L), ... b(Sn, L) }.

In the figure, A(S, L) = {P1, P2, P3}, B(S, L) = {Q1, Q2, Q3}.

We'll call two transversals L1, L2 equivalent if A(S1, L) = A(S2, L).

Definitions:

1) A simple polygon is a kite-shaped if it contains only four convex vertices labeled A, B, C, D such that the diagonals [A, C] and [B, D] lie in the polygon.

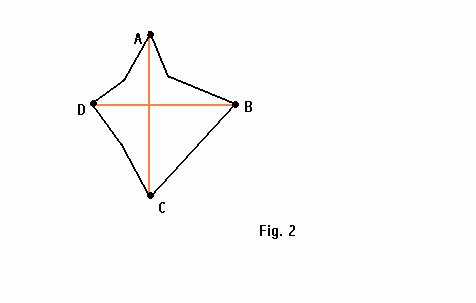
Pay attention that AB, BC, CD and DA are concave chains.

2) A line segment Si is left of another line segment Sj with respect to a transversal L, if the intersection of Si with L lies to the left of the intersection of Sj with L.

The right relation is defined in the same manner.

3) Left-envelope of a set of line segments S is defined with respect to an equivalence class of transversals. It's the union of all points P which are the leftmost intersection points of a line segment in S with some transversal belonging to the class.

The right-envelope is defined similarly.

Let CH(A(S, L)) denote the convex hull of the set of points A(S, L), and CH(B(S, L)) -- the convex hull of B(S, L).

Now we are ready to present an algorithm for computing the shortest transversals:

We are given a set S = {S1, S2, ..., Sn} of line segments.

Transform each line segment in S into a double wedge in the dual plane (Si --> Ri).
Let R = R1 U R2 U ... U Rn be the intersection of the double wedges. If R is empty then exit -- no transversal exists.

As you saw in the preliminaries section, R consists of several (say k) convex regions. Let R_i and R_i+1 be two adjacent convex regions and L(R_i) and L(R_i+1) be two representative transversals. If the two regions share a vertex which is a center of some double wedge (say corresponding to a segment Sk), then it holds that

A(S, L(R_i+1)) = { A(S, L(R_i)) - a(Sk, L(R_i)) } U { b(Sk, L(R_i)) }, and

B(S, L(R_i+1)) = { B(S, L(R_i)) - b(Sk, L(R_i)) } U { a(Sk, L(R_i)) }.

If R_i and R_i+1 are disjoint, the line segments whose end points switch sides from above or below of L(R_i) to below or above of L(R_i+1) are those whose corresponding double wedge centers lie between regions R_i and R_i+1. Therefore, we can compute the sets A and B for L(R_i+1) from those for L(R_i).

For every convex region:

Compute the left envelope, the right envelope, convex hull of the upper end points of S, convex hull of the lower end points of S.

Compute the critical lines of support between the two convex hulls and concatenate their relevant portions with the envelopes and convex hull boundaries to obtain a kite-shaped polygon.

Compute the minimum visible distance between the left and right chains of the polygon.

Select the smallest distance obtained during the previous step and exit with the line segment that determines this distance.