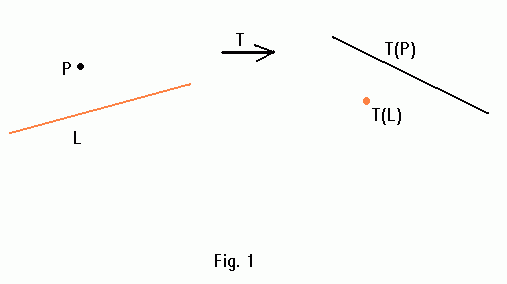
Let's introduce a geometric transform T which maps a point into a line and a line into a point.

P = (a,b) ==> T(P): y = ax + b,

L: y = kx + d ==> T(L) = (-k,d).

Fact 1: T retains the relative positions of points and lines, i.e. a point p lies above a line L iff the point T(L) lies below the line T(P).

Proof:  Let L: y = kx + d; P = (x, y) = (a, b). P lies above L, that is if P1 = (x1, y1) = (x1, k*x1+d)  and P2 = (x2, y2) = (x2, k*x2+d) are two points on L such that x1 > x2, then the signed area of the triangle Area(P1,P2,P) < 0. Let's use a well known formula for calculating the signed area of a triangle:

2*Area(P1,P2,P) = x1*y2 - y1*x2 + x2*y - y2*x + x*y1 - y*x1 = x1*(k*x2+d) - x2*(k*x1+d) + x2*b - a*(k*x2+d) + a*(k*x1+d) - b*x1 = k*x1*x2 + d*x1 - k*x1*x2 - d*x2 + b*x2 - a*k*x2 - a*d + a*k*x1 + a*d - b*x1 = (x1 - x2)*(d + k*a - b) < 0.

According to the assumption, x1 - x2 > 0, therefore d + k*a -b < 0.

Now we'll apply the transform T to P and L:

T(P): y = a*x + b,

T(L)  =  (-k, d).  

As before, we'll compute the signed area of the triangle (P1, P2, T(L)), where P1 = (x1, a*x1+b) and P2 = (x2, a*x2+b) are two points on T(L) such that x1 > x2, and T(L) = (x, y) = (-k, d).

2*Area(P1,P2,T(L)) = x1*(a*x2+b) - x2*(a*x1+b) + x2*d - (-k)*(a*x2+b) + (-k)*(a*x1+b) - d*x1 = -(x1 - x2)*(d + k*a - b). According to the assumptions, x1 - x2 > 0, and d+ k*a - b <0, therefore Area(P1,P2,T(L)) > 0 ==> T(L) lies above T(P).

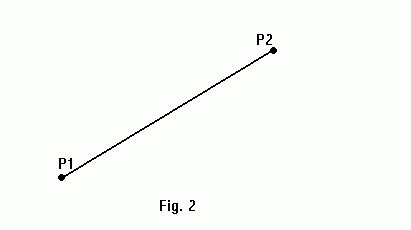
Now when we understand how a point and a line are transformed, let's look at the transform of a line segment. Obviously, a line segment is fully determined by its two endpoints.

Let P1 = (a1, b1) and P2 = (a2, b2) two points determining a line segment S, such that a1 is not equal to a2. We may assume that the segment is not vertical because we can always avoid it by slightly rotating a plane, obtaining the solution in the rotated plane, and then rotating it back.

The transform of the two points P1, P2 represents two intersecting lines (the lines cannot be parallel because a1 and a2 are not equal).

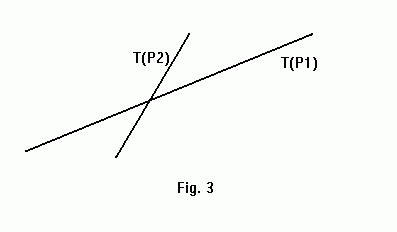
Fact 2: For every point P belonging to the line segment S formed by P1 and P2, the line T(P) intersects T(P1) and T(P2) in their point of intersection.

Proof: Let P1 = (a1, b1), P2 = (a2, b2), P = (a, b). Without loss of generality we may assume that a1 < a2 and b1 < b2. Then, b can be expressed as b = a*(b2-b1)/(a2-a1)-a1*(b2-b1)/(a2-a1)+b1. By solving a simple equation, it's easy to find an intersection point of T(P1) and T(P2):

x = -(b2-b1)/(a2-a1),

y = -a1*(b2-b1)/(a2-a1)+b1.

Obviously, (x, y) belongs to the line T(P): y = a*x + b where b is given by equation above.

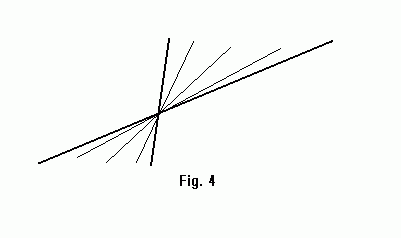
Therefore, S is transformed into the "double wedge" (two opposite wedges whose union doesn't contain a vertical line). The vertical line is not contained, because it corresponds to a point in infinity in the primal plane, which obviously can not belong to the segment.

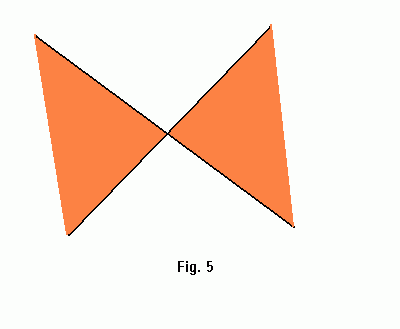
Fact 3: A line L intersects a line segment S with endpoints P1, P2 iff the point T(L) lies in the double wedge T(S).

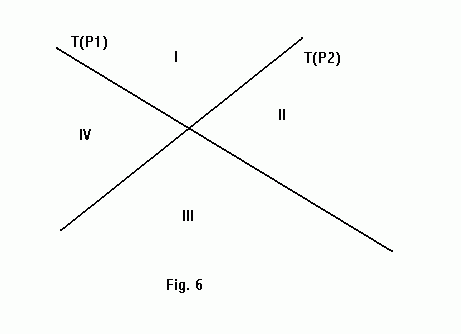
Proof: We assume that L intersects S not in its endpoints P1,P2. L intersects S iff the endpoints of S lie from the opposite sides of L (one above and one below). If you look at the picture above, points in region I lie above both T(P1) and T(P2), points in region III lie below both lines, while those in regions II and IV lie from between the two lines. Pay attention that these regions exactly correspond to the double wedge of the segment formed by P1 and P2.

Now we are ready to characterize the points corresponding to the stabbing line of line segments.

Fact 4:  The set of valid stabbing lines for a set of line segments is transformed into the intersection of their double wedges.

Proof: Follows directly from fact 3.

We call this intersection a "stabbing region". Obviously, all the lines whose transform belongs to the stabbing region, are the stabbing lines of the line segments set. Therefore, we have found an easy characterization of a stabbing line, which is any point in the intersection of double wedges in the transformed plane. 

Lemma 1: The stabbing region for n line segments consists of at most n + 1 convex and potentially unbounded polygons whose orthogonal projections onto the x-axis do not intersect except potentially at their endpoints.

Proof (by induction):

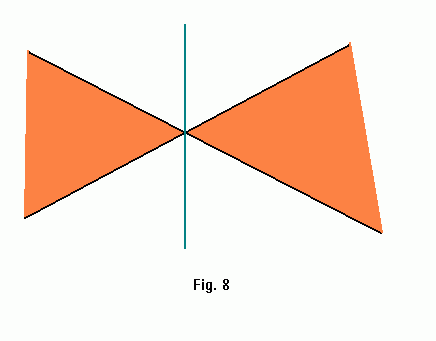
Basis (n=1):  Clearly one line segment corresponds  to one double wedge, which can be separated by a vertical line through its intersection point. This implies that the orthogonal projections onto the x-axis don't intersect, and that the stabbing region consists of n+1=2 unbounded convex polygons (see figure 6).

Induction step: Let's assume the correctness for n line segments, and prove for n+1.

When an additional double wedge is added, its intersection point may or may not fall inside one of the existing convex polygons.

If it indeed falls inside one of the polygons then two convex polygons are created instead.

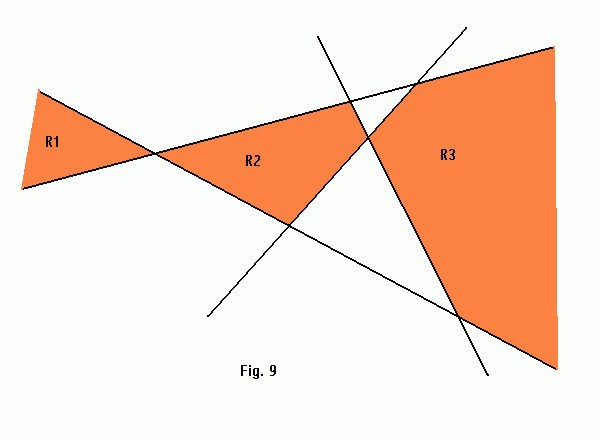
In figure 9, for n = 2 the stabbing regions consists of three convex polygons R1, R2 and R3, two of which are unbounded. Let another double wedge formed by the lines L1, L2 be added:

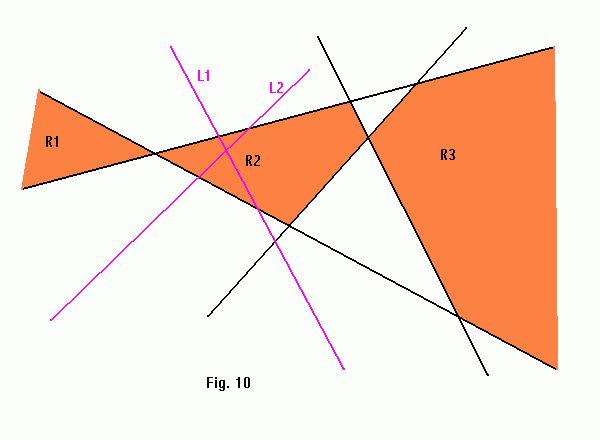
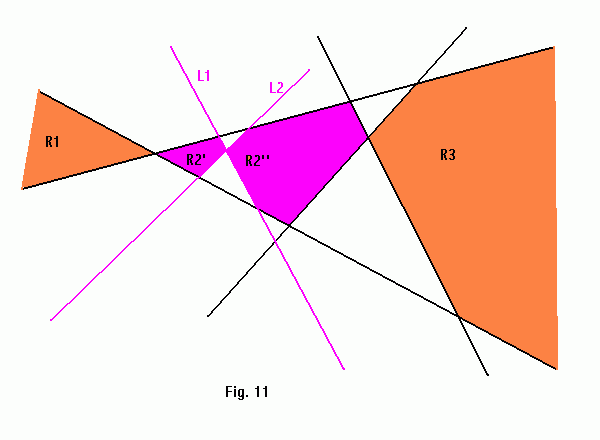
Due to addition of the new double wedge whose intersection point lies inside R2, it's divided into four convex polygons, two of which intersect with the new double wedge and therefore form two new convex stabbing regions:

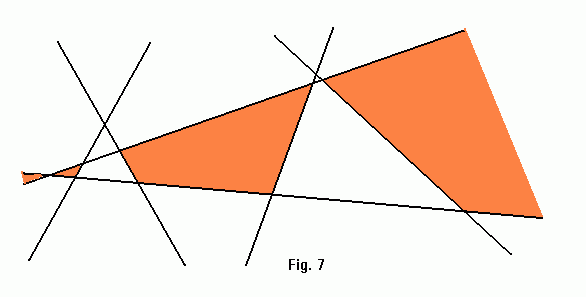
If the intersection point does not fall inside one of the existing polygons (see figure 7) then total number of polygons will either remain the same or will be incremented by 1. In either case, the induction hypothesis holds.